En el
contexto de este capítulo Vd será invitado
también a visitar estos apartados...
El análisis e interpretación de la función de densidad electrónica, es decir, la resolución de una estructura cristalina (molecular, o no molecular), nos conduce a un modelo inicial, no definitivo, que se describe por las posiciones relativas de los átomos, los cuales pueden representarse mediante puntos o pequeñas esferas:



AJUSTE FINAL DEL MODELO
Los parámetros fundamentales asociados a cada átomo en una estructura tridimensional son, obviamente, las tres coordenadas (x, y, z) posicionales de cada átomo referidas a los ejes del sistema de referencia (celdilla elemental). Pero, en general, dada la sobredeterminación experimental que en general proporciona la difracción, el modelo cristalográfico puede permitirse ampliar su complejidad, asociando además a cada átomo un parámetro "térmico" que da cuenta de su estado de vibración térmica isotrópica (esférica) alrededor de su posición de equilibrio y que se vería representado por el mayor o menor volumen de las esferas de la representación gráfica. Por lo tanto el modelo isotrópico está representado por 4 variables: 3 posicionales + 1 térmica (que equivale al radio de la esfera de vibración).
Sin embargo, en el caso de estructuras pequeñas y medianas (hasta algunos centenares de átomos), el experimento de la difracción suele dar de sí para poder completar algo más el modelo de vibración térmica de cada átomo, asignando un tensor (6 variables) a cada posición atómica, que expresa el estado de vibración del átomo de un modo anisotrópico, es decir, distinguiendo entre diferentes direcciones de vibración en forma de elipsoide (que se asemeja a la forma de una pelota de "base-ball"). De este modo, el modelo cristalográfico anisotrópico requiere 9 variables por cada átomo (3 posicionales + 6 vibracionales).




Izquierda: Modelo anisotrópico de la estructura tridimensional de una molécula y de fragmentos de sus vecinas.
Derecha: Modelo anisotrópico de la estructura tridimensional de una molécula y su empaquetamiento en el cristal.
Independientemente del modelo isotrópico o anisotrópico, y debido a la sobreabundancia de datos experimentales de que, normalmente, se dispone a través del experimento de difracción, el resultado cristalográfico tiene capacidad para evolucionar hasta valores posicionales y de vibración térmica muy precisos que redundan en la precisión de cualquier parámetro geométrico que se derive de la estructura (distancias interatómicas, ángulos de enlace, etc.).
La obtención de este modelo "ajustado" (afinado), isotrópico o anisotrópico, es consecuencia de metodología matemática analítica como la de los mínimos cuadrados. Mediante esta técnica se "mueven" ligeramente las posiciones atómicas (las coordenadas) y se aplican factores térmicos a cada átomo de tal modo que el patrón de difracción calculado con dicho modelo sea prácticamente igual que el experimental (observado), es decir que se minimizan las diferencias entre los factores de estructura observados y calculados. Este proceso se lleva a cabo minimizando (haciendo tender a cero) la función:
Aunque la sobredeterminación experimental mencionada suele asegurar el buen término de este proceso matemático de ajuste, éste debe de ser controlado con sentido estereoquímico, es decir, comprobando que los pequeños movimientos posicionales de los átomos sean razonables y que por lo tanto generan distancias interatómicas dentro de lo esperable. Del mismo modo, los factores de vibración térmicos (isotrópicos ó anisotrópicos) asociados a los átomos deben de mostrar valores razonables.
Además del control aludido de los ligeros cambios que sufre el modelo durante este proceso de ajuste, parece obvio que (si todo va bien), además, el patrón de difracción calculado (Fc) con el modelo (coordenadas + factores de vibración) explicará cada vez mejor el patrón de difracción observado (Fo). La comparación entre ambos patrones (observado vs. calculado) se realiza mediante el denominado parámetro R, que define el factor de "desacuerdo" entre ambos patrones:
El valor del factor de desacuerdo (R) suele estimarse en forma porcentual (%), es decir, multiplicado por 100, de tal modo que estructuras bien resueltas y con grado de precisión adecuado muestran un factor R siempre por debajo de 0.10 (10%), lo cual implica que el patrón de difracción calculado difiere del observado (experimental) menos del 10%.
En las estructuras de las macromoléculas (enzimas, proteínas, etc.), es normal que no exista una sobredeterminación de valores experimentales y por lo tanto dificilmente se llegan a usar un modelos estructurales anisotrópicos. En estos casos, además, los valores de desacuerdo (R) son mayores que en el caso de las moléculas pequeñas y medianas, de tal modo que valores del orden del 20%, o algo menores, suelen ser aceptables. Además, como consecuencia de esta escasez relativa de datos experimentales, el procedimiento analítico de ajuste mencionado (mínimos cuadrados) debe de combinarse con un proceso de modelado estereoquímico interactivo e imponiendo ciertas "restricciones suaves" a la geometría de la molécula.
VALIDACIÓN DEL MODELO
Existen una serie de herramientas que ayudan a evaluar la fiabilidad de un modelo estructural, y que en términos cristalográficos se conocen con el nombre de validación, de tal modo que el modelo estructural obtenido debe ser contínuamente contrastado y validado mediante criterios estereoquímicos consistentes. Es decir, las distancias interatómicas y ángulos de enlace deben ser aceptables. No lo sería, por ejemplo, una distancia C---O de 0.8 Angström para un supuesto grupo carbonilo (C=O). Y del mismo modo, los ángulos de enlace, deben de ser consistentes con una geometría aceptable. Estos criterios son muy restrictivos para los modelos estructurales de compuestos de hasta mediana complejidad, pero incluso en las estructuras de las macromoléculas deben de cumplirse unos mínimos


Del mismo modo, los valores de los factores térmicos asociados a cada átomo deben corresponder a valores físicamente aceptables. Estos parámetros vibracionales dan cuenta de la movilidad de diferentes zonas estructurales. Así, en la estructura de una macromolécula, éstos valores deben ser coherentes con las zonas internas o externas de la molécula, siendo en general menores para el interior, y mayores para las zonas externas, próximas al solvente.

GRADO DE FIABILIDAD DEL MODELO
Un modelo que ha sido "validado" de acuerdo con los criterios descritos, es decir, que muestra:
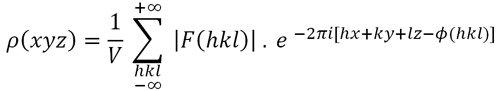
Pero en cualquiera de los casos, el cristalógrafo llega a parámetros atómicos (posicionales y vibracionales) con su correspondiente valor de precisión. Este hecho provoca que cualquier parámetro cristalográfico directo (coordenadas atómicas y factores de vibración) o indirecto (distancias, ángulos, etc.) se exprese como un valor numérico seguido de otro (entre paréntesis) que expresa la denominada desviación estándard del anterior y que afecta a la última cifra del valor expresado. Por ejemplo, una distancia interatómica expresada en Angströms como 1.541 (2) implica un valor numérico de 1.541 y una desviación estándard de 0.002.
LA CONFIGURACIÓN (O ESTEREOQUIMICA) ABSOLUTA
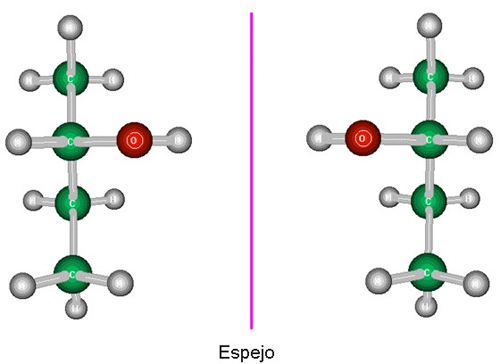
Ya se ha comentado en un apartado anterior que en todas aquellas estructuras en las que no existen planos de simetría ni centros de inversión se puede hablar de "configuración absoluta", es decir que la estructura en cuestión es diferente de su imagen especular:
Pues bien, este matiz o diferencia estructural, que es de vital importancia en lo que las propiedades moleculares se refiere, puede asignarse inequívocamente a través del proceso de difracción en los cristales (sin necesidad de recurrir a patrones), gracias a la denominada dispersión anómala que algunos átomos presentan frente a la radiación X y que además ha dado pie a la aparición de una metodología de resolución en el caso de las macromoléculas. No parece dificil comprender el hecho de que los enantiómeros de una molécula tengan propiedades desiguales, ya que en definitiva se trata de moléculas diferentes, pero en el caso de la actividad biológica este aspecto resulta especialmente llamativo.
La señal experimental en difracción que nos permite esta diferenciación estructural es consecuencia de
En estas condiciones deja de cumplirse la ley de Friedel y por lo tanto los factores de estructura, tales como |Fh,k,l | y |F-h,-k,-l |, serán "algo diferentes". Por lo tanto, la comparación de los denominados estimadores de Bijvoet, es decir la comparación de los cocientes entre factores de estructura observados para tales parejas, frente a los correspondientes cocientes entre factores de estructura calculados con uno de los dos posibles modelos absolutos, deben de mantener idéntico sesgo:
es decir, que si un determinado cociente entre valores observados es menor de la unidad, también debe de ocurrir así para el mismo cociente entre factores calculados, y alternativamente al revés, y todo ello para un elevado número de cocientes.
En el caso de que los cocientes entre valores observados tenga un comportamiento contrario a los cocientes entre valores calculados, sería señal inequívoca de que nuestro modelo absoluto es el erróneo, debiendo ser modificado de manera coherente.
El lector aventajado puede también consultar el contenido de este enlace sobre dispersión anómala, preparado por Ethan A. Merritt.
RESULTADO FINAL
El conjunto de información que describe un modelo cristalográfico final es muy concreto:

El análisis e interpretación de la función de densidad electrónica, es decir, la resolución de una estructura cristalina (molecular, o no molecular), nos conduce a un modelo inicial, no definitivo, que se describe por las posiciones relativas de los átomos, los cuales pueden representarse mediante puntos o pequeñas esferas:



Izquierda:
Modelo
inicial de la estructura
tridimensional de una molécula.
Los átomos están representados por
pequeñas
esferas.
Centro: Modelo inicial de la estructura tridimensional de una molécula. A pesar de la mayor o menor belleza del modelo, la cantidad de información es prácticamente la misma que en el modelo de la izquierda.
Derecha: Modelo inicial de la estructura tridimensional de una molécula, incluyendo la estructura cristalina (empaquetamiento). La visión muestra los ejes de la celdilla elemental.
Centro: Modelo inicial de la estructura tridimensional de una molécula. A pesar de la mayor o menor belleza del modelo, la cantidad de información es prácticamente la misma que en el modelo de la izquierda.
Derecha: Modelo inicial de la estructura tridimensional de una molécula, incluyendo la estructura cristalina (empaquetamiento). La visión muestra los ejes de la celdilla elemental.
Pero
una vez conseguido el modelo estructural completo, con
total
sentido estereoquímico e incluyendo el empaquetamiento
cristalino, es necesario sacar el máximo
partido a las medidas experimentales, ya que, en general, se dispone de
una cierta sobredeterminación de la información
experimental (patrón de difracción).
Por
ejemplo, para una estructura de tamaño mediano, con unos 50
átomos independientes (en la unidad asimétrica,
es decir,
en la parte que se repite por las operaciones de simetría)
normalmente se dispone de hasta aproximadamente 2.500
factores
de estructura, lo que
supone disponer de hasta 50
observaciones por
átomo. Este superávit de información
experimental normalmente no llega hasta estos límites en el
caso de
estructuras
más complejas, tal como ocurre en el caso de las
macromoléculas.
AJUSTE FINAL DEL MODELO
Los parámetros fundamentales asociados a cada átomo en una estructura tridimensional son, obviamente, las tres coordenadas (x, y, z) posicionales de cada átomo referidas a los ejes del sistema de referencia (celdilla elemental). Pero, en general, dada la sobredeterminación experimental que en general proporciona la difracción, el modelo cristalográfico puede permitirse ampliar su complejidad, asociando además a cada átomo un parámetro "térmico" que da cuenta de su estado de vibración térmica isotrópica (esférica) alrededor de su posición de equilibrio y que se vería representado por el mayor o menor volumen de las esferas de la representación gráfica. Por lo tanto el modelo isotrópico está representado por 4 variables: 3 posicionales + 1 térmica (que equivale al radio de la esfera de vibración).
Sin embargo, en el caso de estructuras pequeñas y medianas (hasta algunos centenares de átomos), el experimento de la difracción suele dar de sí para poder completar algo más el modelo de vibración térmica de cada átomo, asignando un tensor (6 variables) a cada posición atómica, que expresa el estado de vibración del átomo de un modo anisotrópico, es decir, distinguiendo entre diferentes direcciones de vibración en forma de elipsoide (que se asemeja a la forma de una pelota de "base-ball"). De este modo, el modelo cristalográfico anisotrópico requiere 9 variables por cada átomo (3 posicionales + 6 vibracionales).


Izquierda: Representación
gráfica de tres
átomos enlazados mediante los modelos de
vibración termica
isotrópica
Derecha: Los mismos átomos de la figura de la izquierda, pero representados mediante el modelo de vibración termica anisotrópica
Derecha: Los mismos átomos de la figura de la izquierda, pero representados mediante el modelo de vibración termica anisotrópica


Izquierda: Modelo anisotrópico de la estructura tridimensional de una molécula y de fragmentos de sus vecinas.
Derecha: Modelo anisotrópico de la estructura tridimensional de una molécula y su empaquetamiento en el cristal.
Independientemente del modelo isotrópico o anisotrópico, y debido a la sobreabundancia de datos experimentales de que, normalmente, se dispone a través del experimento de difracción, el resultado cristalográfico tiene capacidad para evolucionar hasta valores posicionales y de vibración térmica muy precisos que redundan en la precisión de cualquier parámetro geométrico que se derive de la estructura (distancias interatómicas, ángulos de enlace, etc.).
La obtención de este modelo "ajustado" (afinado), isotrópico o anisotrópico, es consecuencia de metodología matemática analítica como la de los mínimos cuadrados. Mediante esta técnica se "mueven" ligeramente las posiciones atómicas (las coordenadas) y se aplican factores térmicos a cada átomo de tal modo que el patrón de difracción calculado con dicho modelo sea prácticamente igual que el experimental (observado), es decir que se minimizan las diferencias entre los factores de estructura observados y calculados. Este proceso se lleva a cabo minimizando (haciendo tender a cero) la función:
Σ
w |
|Fo| - |Fc|
|2
→ 0
Función de mínimos cuadrados que se utiliza para ajustar el modelo final de las estructuras
Función de mínimos cuadrados que se utiliza para ajustar el modelo final de las estructuras
en
donde w
representa un factor de "peso" asignado a cada observación,
separando así los efectos de aquellas observaciones
más precisas de las menos precisas y evitando así
errores sistemáticos en las observaciones experimentales que
pudieran sesgar el modelo.
Fo
y Fc
representan los factores de estructura observados y calculados,
respectivamente.
El ajuste consiste en modificar ligeramente las coordenadas de los
átomos del modelo para conseguir que los factores de
estructura
calculados (Fc)
con dicho modelo se parezcan los más posible a los factores
de estructura observados en el experimento de difracción (Fo).
Aunque la sobredeterminación experimental mencionada suele asegurar el buen término de este proceso matemático de ajuste, éste debe de ser controlado con sentido estereoquímico, es decir, comprobando que los pequeños movimientos posicionales de los átomos sean razonables y que por lo tanto generan distancias interatómicas dentro de lo esperable. Del mismo modo, los factores de vibración térmicos (isotrópicos ó anisotrópicos) asociados a los átomos deben de mostrar valores razonables.
Además del control aludido de los ligeros cambios que sufre el modelo durante este proceso de ajuste, parece obvio que (si todo va bien), además, el patrón de difracción calculado (Fc) con el modelo (coordenadas + factores de vibración) explicará cada vez mejor el patrón de difracción observado (Fo). La comparación entre ambos patrones (observado vs. calculado) se realiza mediante el denominado parámetro R, que define el factor de "desacuerdo" entre ambos patrones:
R =
Σ [
| |Fo| - |Fc|
| ] / |Fo|
Factor de desacuerdo del modelo estructural, estimado en función de las diferencias entre los factores de estructura observados y los calculados con el modelo final
Factor de desacuerdo del modelo estructural, estimado en función de las diferencias entre los factores de estructura observados y los calculados con el modelo final
El valor del factor de desacuerdo (R) suele estimarse en forma porcentual (%), es decir, multiplicado por 100, de tal modo que estructuras bien resueltas y con grado de precisión adecuado muestran un factor R siempre por debajo de 0.10 (10%), lo cual implica que el patrón de difracción calculado difiere del observado (experimental) menos del 10%.
En las estructuras de las macromoléculas (enzimas, proteínas, etc.), es normal que no exista una sobredeterminación de valores experimentales y por lo tanto dificilmente se llegan a usar un modelos estructurales anisotrópicos. En estos casos, además, los valores de desacuerdo (R) son mayores que en el caso de las moléculas pequeñas y medianas, de tal modo que valores del orden del 20%, o algo menores, suelen ser aceptables. Además, como consecuencia de esta escasez relativa de datos experimentales, el procedimiento analítico de ajuste mencionado (mínimos cuadrados) debe de combinarse con un proceso de modelado estereoquímico interactivo e imponiendo ciertas "restricciones suaves" a la geometría de la molécula.
VALIDACIÓN DEL MODELO
Existen una serie de herramientas que ayudan a evaluar la fiabilidad de un modelo estructural, y que en términos cristalográficos se conocen con el nombre de validación, de tal modo que el modelo estructural obtenido debe ser contínuamente contrastado y validado mediante criterios estereoquímicos consistentes. Es decir, las distancias interatómicas y ángulos de enlace deben ser aceptables. No lo sería, por ejemplo, una distancia C---O de 0.8 Angström para un supuesto grupo carbonilo (C=O). Y del mismo modo, los ángulos de enlace, deben de ser consistentes con una geometría aceptable. Estos criterios son muy restrictivos para los modelos estructurales de compuestos de hasta mediana complejidad, pero incluso en las estructuras de las macromoléculas deben de cumplirse unos mínimos

Dispersión máxima
aceptable para distancias interatómicas y ángulos
de enlace en un modelo estructural de una macromolécula
Igualmente,
en el caso de las proteínas, debido al
carácter geométrico del
enlace peptídico (enlace entre dos aminoácidos
consecutivos), debe de cumplirse que el ángulo de
torsión en dicho enlace no debe desviarse mucho del
valor aceptable para la conformación estructural que adoptan
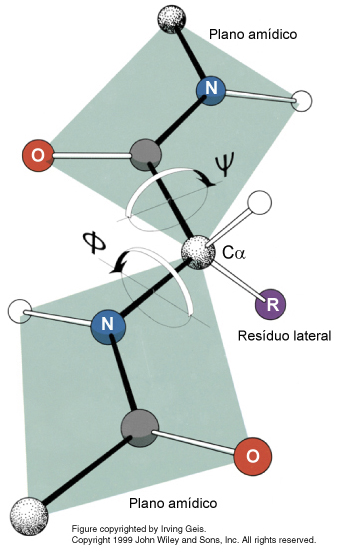
esos aminoácidos, tal como se muestra en la denominada
distribución de Ramachandran:

Izquierda: Esquema
del enlace peptídico,
mostrando los dos ángulos de torsión (Ψ y Φ) que
lo
definen. Pueden observarse también estos ángulos pinchando
en este enlace.
Derecha: Plot de Ramachandran: Zonas de dispersión aceptable para los valores de los ángulos de torsión de los enlaces peptídicos en un modelo estructural de una macromolécula, dependiendo de las diferentes zonas estructurales (alfa-hélices, láminas-beta, etc.)
Derecha: Plot de Ramachandran: Zonas de dispersión aceptable para los valores de los ángulos de torsión de los enlaces peptídicos en un modelo estructural de una macromolécula, dependiendo de las diferentes zonas estructurales (alfa-hélices, láminas-beta, etc.)
Del mismo modo, los valores de los factores térmicos asociados a cada átomo deben corresponder a valores físicamente aceptables. Estos parámetros vibracionales dan cuenta de la movilidad de diferentes zonas estructurales. Así, en la estructura de una macromolécula, éstos valores deben ser coherentes con las zonas internas o externas de la molécula, siendo en general menores para el interior, y mayores para las zonas externas, próximas al solvente.

Representación
gráfica de la cadena principal de una
macromolécula en
donde los colores muestran los factores de
vibración
térmica. Colores "fríos"
(azules)
denotan zonas de escasa movilidad. Colores "calientes" (verdes
y rojos)
denotan zonas mucho más móviles.
GRADO DE FIABILIDAD DEL MODELO
Un modelo que ha sido "validado" de acuerdo con los criterios descritos, es decir, que muestra:
- acuerdo razonable entre los módulos de los factores de estructura observados (experimentales) y calculados,
- distancias interatómicas, ángulos de enlace y ángulos de torsión aceptables, es decir que cumple con criterios esteroquímicos aceptables, y
- factores de vibración térmica físicamente razonables,
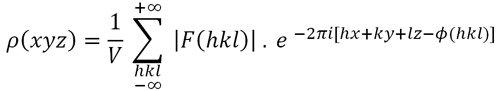
sobre
la cual se han posicionado unos átomos, y en la cual
influyen una serie de condicionamientos que se describen en
otro apartado, que invitamos a visitar.
Pero en cualquiera de los casos, el cristalógrafo llega a parámetros atómicos (posicionales y vibracionales) con su correspondiente valor de precisión. Este hecho provoca que cualquier parámetro cristalográfico directo (coordenadas atómicas y factores de vibración) o indirecto (distancias, ángulos, etc.) se exprese como un valor numérico seguido de otro (entre paréntesis) que expresa la denominada desviación estándard del anterior y que afecta a la última cifra del valor expresado. Por ejemplo, una distancia interatómica expresada en Angströms como 1.541 (2) implica un valor numérico de 1.541 y una desviación estándard de 0.002.
LA CONFIGURACIÓN (O ESTEREOQUIMICA) ABSOLUTA
Ya se ha comentado en un apartado anterior que en todas aquellas estructuras en las que no existen planos de simetría ni centros de inversión se puede hablar de "configuración absoluta", es decir que la estructura en cuestión es diferente de su imagen especular:

Modelos estructurales de dos
moléculas enantiómeras entre sí (una
es imagen especular de
la
otra)
Pues bien, este matiz o diferencia estructural, que es de vital importancia en lo que las propiedades moleculares se refiere, puede asignarse inequívocamente a través del proceso de difracción en los cristales (sin necesidad de recurrir a patrones), gracias a la denominada dispersión anómala que algunos átomos presentan frente a la radiación X y que además ha dado pie a la aparición de una metodología de resolución en el caso de las macromoléculas. No parece dificil comprender el hecho de que los enantiómeros de una molécula tengan propiedades desiguales, ya que en definitiva se trata de moléculas diferentes, pero en el caso de la actividad biológica este aspecto resulta especialmente llamativo.
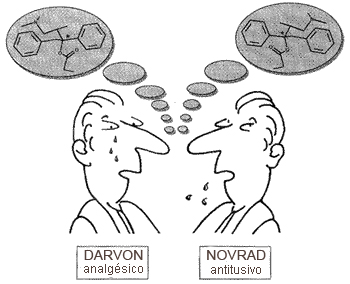 Las
moléculas enantiómeras que se representan en la
figura de
la izquierda fueron puestas en el mercado por una empresa
farmacéutica y, obviamente, éstas mostraron
propiedades
diferentes. Las
moléculas enantiómeras que se representan en la
figura de
la izquierda fueron puestas en el mercado por una empresa
farmacéutica y, obviamente, éstas mostraron
propiedades
diferentes. Las propiedades de DARVON (Dextropropoxyphene Napsylate) pueden consultarse a través de este enlace, mientras que NOVRAD (Levopropoxyphene Napsylate) fue retirada del mercado. |
La señal experimental en difracción que nos permite esta diferenciación estructural es consecuencia de
En estas condiciones deja de cumplirse la ley de Friedel y por lo tanto los factores de estructura, tales como |Fh,k,l | y |F-h,-k,-l |, serán "algo diferentes". Por lo tanto, la comparación de los denominados estimadores de Bijvoet, es decir la comparación de los cocientes entre factores de estructura observados para tales parejas, frente a los correspondientes cocientes entre factores de estructura calculados con uno de los dos posibles modelos absolutos, deben de mantener idéntico sesgo:
es decir, que si un determinado cociente entre valores observados es menor de la unidad, también debe de ocurrir así para el mismo cociente entre factores calculados, y alternativamente al revés, y todo ello para un elevado número de cocientes.
En el caso de que los cocientes entre valores observados tenga un comportamiento contrario a los cocientes entre valores calculados, sería señal inequívoca de que nuestro modelo absoluto es el erróneo, debiendo ser modificado de manera coherente.
El lector aventajado puede también consultar el contenido de este enlace sobre dispersión anómala, preparado por Ethan A. Merritt.
RESULTADO FINAL
El conjunto de información que describe un modelo cristalográfico final es muy concreto:
- Datos sobre el experimento de difracción que nos condujo al modelo: longitud de onda de los rayos X y el patrón de difracción obtenido (la intensidad e indices hkl de los miles, o hasta cientos de miles) de las ondas dispersadas por el cristal,
- Dimensiones de la celdilla elemental (calculadas a partir de la celdilla recíproca),
- Simetría del cristal (también deducida de la simetría del espacio recíproco), y
- Un conjunto de datos que expresan la posición de cada átomo en la estructura, su estado de vibración térmica y, en su caso el denominado factor de ocupación (ó de población), tal como muestra la siguiente tabla.

Fragmento del
resultado cristalográfico de la estructura de una
proteína, expresado en el denominado formato "tipo PDB"
(Protein Data Bank), es
decir con coordenadas atómicas expresadas en
Angström y
referidas a un sistema de ejes ortogonales, diferentes de los
cristalogáficos.
Para mayor claridad de la tabla se han omitido las
estimaciones
de precisión de las coordenadas y de los restantes
datos
que afectan al átomo y que siempre forman parte del
resultado.
El factor de población expresa la "fracción de átomo" localizada en una posición concreta y normalmente este factor es la unidad. Pero el siginificado de este parámetro requiere una aclaración para el lector principiante, ya que se podría llegar a pensar que existen "fracciones de átomo", lo que carace de significado físico. Habida cuenta de que las moléculas tienen sus movimientos, de que el experimento de difracción no es instantáneo y que, por otra parte, los rayos X "ven" una enorme cantidad de celdillas elementales, parece razonable pensar que un factor de población menor de la unidad representa el hecho de que, en una cierta cantidad significativa de celdillas, el átomo ha cambiado de posición, y por lo tanto el resultado cristalográfico está "viendo", como promedio (en tiempo y celdilla), sólo una fracción del átomo en la posición dada por las correspondientes coordenadas.
Las coordenadas atómicas, y en general toda la información extraída de un estudio cristalográfico, se almacena en bases de datos accesibles, algo diferentes según el tipo de compuesto o molécula y que se comentarán en otro capítulo de estas páginas.
REPRESENTACIONES GRÁFICAS DEL MODELO
Pero, además, las técnicas actuales de representación gráfica permiten obtener modelos de una gran belleza y capacidad descriptiva para que el lector pueda visualizar y comprender las estructuras, tal como demuestran algunos de los ejemplos que se muestran a continuación:


Izquierda: Modelo de bolas y barras para representar la estructura de un compuesto inorgánico simple
Derecha: Representación para otro compuesto inorgánico, al cual se le ha añadido una representación poliédrica parcial




Finalmente, haciendo uso de información adicional de otras técnicas (como la crio-microscopía electrónica), o simplemente combinando dos modelos moleculares en diferentes conformaciones, se pueden obtener modelos como los mostrados a continuación. Más aún, utilizando los tiempos de exposición ultracortos de los rayos X producidos por los láseres de electrones libres, los cristalógrafos son capaces de recopilar datos de difracción de macromoléculas en diferentes conformaciones, es decir, durante el transcurso de sus respectivas tareas. De esta manera, utilizando una gran cantidad de instantáneas de rayos X, podemos producir como una película donde podemos seguir las modificaciones moleculares y, por lo tanto, comprender su función.


El factor de población expresa la "fracción de átomo" localizada en una posición concreta y normalmente este factor es la unidad. Pero el siginificado de este parámetro requiere una aclaración para el lector principiante, ya que se podría llegar a pensar que existen "fracciones de átomo", lo que carace de significado físico. Habida cuenta de que las moléculas tienen sus movimientos, de que el experimento de difracción no es instantáneo y que, por otra parte, los rayos X "ven" una enorme cantidad de celdillas elementales, parece razonable pensar que un factor de población menor de la unidad representa el hecho de que, en una cierta cantidad significativa de celdillas, el átomo ha cambiado de posición, y por lo tanto el resultado cristalográfico está "viendo", como promedio (en tiempo y celdilla), sólo una fracción del átomo en la posición dada por las correspondientes coordenadas.
Las coordenadas atómicas, y en general toda la información extraída de un estudio cristalográfico, se almacena en bases de datos accesibles, algo diferentes según el tipo de compuesto o molécula y que se comentarán en otro capítulo de estas páginas.
REPRESENTACIONES GRÁFICAS DEL MODELO
 Del
modelo estructural final (coordenadas de los átomos, etc.)
se deriva directamente todo un conjunto de información
adicional que conduce al conocimiento detallado
de la estructura en sí, tales como son las distancias
interatómicas, ángulos de enlace,
ángulos de
torsión, planos moleculares, momento dipolar..., y en
general
cualquier detalle que pueda ser de utilidad para la
comprensión
de la funcionalidad y/o propiedades del material objeto del estudio,
sea éste de naturaleza molecular o no. Del
modelo estructural final (coordenadas de los átomos, etc.)
se deriva directamente todo un conjunto de información
adicional que conduce al conocimiento detallado
de la estructura en sí, tales como son las distancias
interatómicas, ángulos de enlace,
ángulos de
torsión, planos moleculares, momento dipolar..., y en
general
cualquier detalle que pueda ser de utilidad para la
comprensión
de la funcionalidad y/o propiedades del material objeto del estudio,
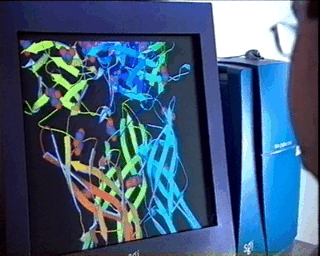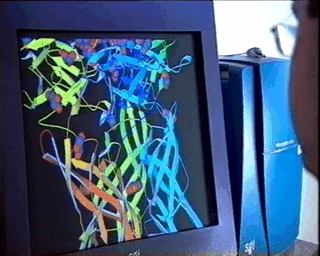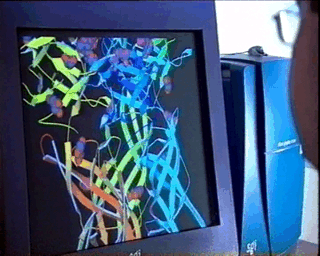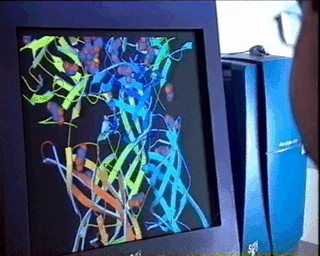
sea éste de naturaleza molecular o no.Especialmente en el caso de moléculas biológicas complejas, el uso de procesadores gráficos de alta calidad y de modelos relativamente simples, facilita mucho la comprensión de las relaciones entre estructura y funcionalidad, tal como se muestra en la figura de la izquierda. |
Pero, además, las técnicas actuales de representación gráfica permiten obtener modelos de una gran belleza y capacidad descriptiva para que el lector pueda visualizar y comprender las estructuras, tal como demuestran algunos de los ejemplos que se muestran a continuación:


Izquierda: Modelo de bolas y barras para representar la estructura de un compuesto inorgánico simple
Derecha: Representación para otro compuesto inorgánico, al cual se le ha añadido una representación poliédrica parcial


Izquierda:
Modelo de bastones,
animado, para representar la estructura molecular y
empaquetamiento de un compuesto orgánico simple
Derecha: En el caso de las moléculas biológicas, dada su complejidad, se suelen usar modelos simplificados, como éste de cintas que representa diferentes motivos estructurales típicos (alfa-hélices, hebras-beta, etc.)
Derecha: En el caso de las moléculas biológicas, dada su complejidad, se suelen usar modelos simplificados, como éste de cintas que representa diferentes motivos estructurales típicos (alfa-hélices, hebras-beta, etc.)


Izquierda:
Modelo
combinado de cintas y bastones para representar la
estructura dimérica de una proteína que
muestra un
ión sulfato en el interior representado mediante bolas
Derecha: Representación de la superficie de una molécula biológica en donde los colores representan diferentes propiedades de hidrofobicidad. La flecha representa el momento dipolar de la molécula
Derecha: Representación de la superficie de una molécula biológica en donde los colores representan diferentes propiedades de hidrofobicidad. La flecha representa el momento dipolar de la molécula
Finalmente, haciendo uso de información adicional de otras técnicas (como la crio-microscopía electrónica), o simplemente combinando dos modelos moleculares en diferentes conformaciones, se pueden obtener modelos como los mostrados a continuación. Más aún, utilizando los tiempos de exposición ultracortos de los rayos X producidos por los láseres de electrones libres, los cristalógrafos son capaces de recopilar datos de difracción de macromoléculas en diferentes conformaciones, es decir, durante el transcurso de sus respectivas tareas. De esta manera, utilizando una gran cantidad de instantáneas de rayos X, podemos producir como una película donde podemos seguir las modificaciones moleculares y, por lo tanto, comprender su función.


Izquierda:
Modelo
combinado entre la
estructura molecular de una proteína y la envolvente que
suministra la microscopía electrónica
de alta
resolución para mostrar un poro formado por la
asociación
de cuatro moléculas de proteína
Derecha: Modelo simplificado que muestra los cambios estructurales de la cadena principal de un enzima, entre sus dos estados: activo (abierto) e inactivo (cerrado). Las dos estructuras límite (las de ambos estados) fueron determinadas mediante cristalografía
Derecha: Modelo simplificado que muestra los cambios estructurales de la cadena principal de un enzima, entre sus dos estados: activo (abierto) e inactivo (cerrado). Las dos estructuras límite (las de ambos estados) fueron determinadas mediante cristalografía


