La
resolución de la estructura de un cristal, mediante
cualquiera de los métodos
descritos, requiere el
conocimiento previo de:
- La composición química aproximada de
su contenido,
- Las dimensiones de la celdilla elemental, deducibles a partir del
patrón de diifracción,
- La simetría
del cristal, deducible
a partir de la simetría de la
difracción (objeto de este subcapítulo), y
- Las intensidades
de difracción
No
es objeto de estas páginas comentar sobre el conocimiento de
la
composición de los cristales, y sobre los aspectos 2, 3 y 4
ya
se ha dado cierta información en otros apartados de estas
páginas. Pero desde el punto de vista práctico al
lector
no le habrá pasado desapercibido que, si bien se ha hablado
de la
simetría
interna de los cristales, poco o nada se ha dicho de cómo
determinar esa simetría interna,
ya que obviamente la inspección visual de un cristal poco
nos
dice en relación con las operaciones de simetría
internas
mediante las cuales se empaquetan sus componentes (átomos,
iones
y moléculas).
Muy probablemente, el lector también se
habrá dado cuenta de que la
única
información fiable con la que cuenta el
cristalógrafo, en
términos de simetría, es la del propio
patrón de
difracción y que
por lo
tanto el problema será deducir la simetría
cristalina a partir
del conocimiento sobre la red recíproca (el
patrón de difracción). Y en efecto, no es
descabellado pensar
que la
simetría
del cristal deje algún tipo de huella en el
patrón de
difracción. Lo vemos...
LEY
DE FRIEDEL
Puede haber, sin embargo, una cierta confusión en
relación con una de las posibles operaciones que configuran
la simetría de un cristal, y esa es la operación
de centro
de simetría. La existencia del centro de
simetría en el cristal no puede inferirse de la existencia
de éste en el patrón de difracción,
porque el
espacio recíproco (el patrón de
difracción) es
siempre centrosimétrico, tal como dedujo el
francés Georges
Friedel (1865-1933), con la ley de su nombre (ley
de Friedel).
Izquierda:
Representación
de la ley de
Friedel en términos de colores que representan
las intensidades de los puntos recíprocos alrededor
del origen. Colores iguales representan intensidades
idénticas
Derecha:
La
ley de Friedel
en
términos del modelo de Bragg, que equivale a decir
que un
espejo refleja del mismo modo por ambos lados.
La
ley de Friedel
establece que las
intensidades asociadas
a dos puntos recíprocos tales como (h,
k, l) y (-h, -k, -l) son
prácticamente iguales. Es decir:
I
(h, k, l) ≈ I (-h, -k, -l)
lo cual equivale a afirmar
que la red recíproca es siempre
centrosimétrica, y por lo tanto la simetría
"aparente" de los cristales es una de los 11
Grupos de Laue.
Una pareja de
reflexiones tales como (h,
k, l) y (-h, -k, -l) se denomina "par de Friedel" y en
presencia de dispersión
anómala muestran una ligera
diferencia en intensidad que puede ser usada tanto para determinar la configuración
absoluta
de las moléculas como para resolver el
problema de las fases por medio del método
MAD.
Como consecuencia de la ley de Friedel se puede afirmar que, en
general,
la simetría
del cristal es menor que la de su patrón de
difracción, es decir, que nos enfrentamos a una
cierta
indeterminación
cuando tratamos de determinar la simetría de un cristal a
partir
del experimento de difracción.
En efecto, si bien los cristales pueden tener (o no) un centro de
simetría que relacione entre sí sus diferentes
componentes (átomos, iones, moléculas), su
patrón
de difracción (la red recíproca) "parece" ser
siempre
centrosimétrica.
Sin embargo, por suerte,
existen algunas operaciones de
simetría
en el cristal que dejan una huella
en el espacio
recíproco. Dicha marca o huella consiste en anular o extinguir
algunas intensidades (puntos
recíprocos) de
un modo sistemático, reconocible mediante
reglas sencillas, y de ahí su nombre de extinciones
sistemáticas.
Las operaciones de simetría que generan las extinciones
sistemáticas son todas aquellas que
contienen una parte translacional, y las más importantes son:
La lista completa de las posibles extinciones sistemáticas y
de
los correspondientes elementos de simetría que las genera
puede
obtenerse desde múltiples fuentes, y
también
aquí, como reproducción de una edición
antigua de las Tablas Internacionales de Cristalografía.
REDES CENTRADAS
Supongamos que disponemos de un retículo cristalino tal como el de la figura de abajo (a la
izquierda), de ejes a
y b.
A esta red se la denomina primitiva, porque que
tiene un
único nudo en el interior de la celdilla, aunque en
realidad
sea en
forma de 4 "cuartos" de nudo.
Si por cualquier
razón hemos
interpretado dicho retículo cristalino en
términos de los ejes A
y B
(figura de la derecha), estaremos eligiendo lo que denominamos una red
centrada (no primitiva) porque contiene más de un nudo
recíproco en el
interior de la celdilla.
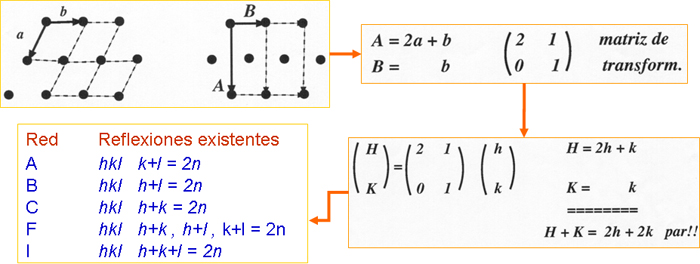
La
transformación de ejes
inherente a este cambio vendrá dado por la que se muestra a
la derecha del dibujo, ya que el eje A
se puede obtener vectorialmente del modo mostrado (2a + b),
y el eje B
es idéntico al b.
y dicha transformación puede representarse por la matriz de
transformación mostrada (tomando como elementos de la matriz
los coeficientes de los segundos miembros de las ecuaciones).
Pues bien, esa misma
matriz de transformación es la que
aplica al cambio de índices de las intensidades de
difracción, de tal modo que aplicándola a los
índices de la red primitiva (h,
k)
se obtendrán los de la red centrada (H,
K)
y si resolvemos dicho producto de matrices y sumamos miembro a miembro,
nos encontramos con el hecho de que la suma de los índices
de la red centrada siempre da lugar a un número par, o dicho
de otro modo, los nudos de la red recíproca cuya suma de
índices H+K
es impar no serán visibles (no hay intensidad).
En la práctica lo que ocurre es que cuando interpretamos un
patrón de difracción estamos definiendo los
índices de las reflexiones en términos de unos
ejes recíprocos (y en definitiva también
directos) y si observamos cualquier tipo de ausencia
o extinción sistemática como la
descrita (o parecida), podremos concluir que estamos ante la
elección de una red centrada, lo cual ya supone una
indicación clara sobre la simetría del cristal
(selección del Grupo Espacial). En nuestro caso particular
podemos concluir que estamos ante una red centrada de tipo C.
EJES
HELICOIDALES
Los
ejes
helicoidales, como el helicoidal binario mostrado en la figura de la
izquierda, son
también
responsables de huellas claras en el patrón de
difracción, también en el sentido de extinguir
sistemáticamente determinados puntos
recíprocos (anular ciertas intensidades). La
explicación
es sencilla si se expresa el factor de estructura asociado a las
reflexiones de un cristal que contenga la pareja de
átomos del dibujo. Los factores de estructura
serán
consecuencia de las dispersiones de cada átomo:
F
= ƒ
cos 2π
( hx + ky + lz ) + ƒ cos 2π ( - hx - ky + l
[(1/2) + z] )
Pero teniendo en cuenta la conocida suma de cosenos:
cos a + cos b = 2
[cos (a+b)/2 ] [cos (a-b)/2]
la expresión anterior se puede escribir como::
F
= 2 ƒ
[cos π (2 l
z + l/2)]
[cos π (2hx
+ 2ky -
l/2)]
lo cual implica que para reflexiones del tipo
00l el
factor de estructura se anula (
F=0)
si
l=2n+1
Generalizando,
y dependiendo del tipo de eje helicoidal, y de su dirección,
nos podemos encontrar con diferentes extinciones
sistemáticas
que, observadas en la práctica nos indican la existencia de
este tipo de operaciones de simetría en el cristal y para el
caso de los ejes helicoidales binarios son:
Eje
helicoidal binario Reflexiones
paralelo a:
existentes:
a
h00 h=2n
b
0k0
h=2n
c
00l
h=2n
Para otras extinciones sistemáticas producidas por otros
ejes helicoidales se puede consultar
la tabla que se ofrece mediante
este enlace. Ver también las
International Tables for X-ray
Crystallography.
PLANOS
DE DESLIZAMIENTO
Los
planos de
simetría que implican traslación, es decir, los
planos de deslizamiento, son igualmente responsables de
extinciones
sistemáticas, de tal modo que si en el
patrón de
difracción observamos que ciertas reflexiones localizadas en
un plano de la red recíproca sólo
están presentes si la suma de sus
índices es par, es porque en el cristal existen
planos
de
deslizamiento, como
por ejemplo:
Plano de
deslizam.:
Reflexiones
perpendicular
a: Translación:
existentes:
a
b/2
0kl
k = 2n
a
c/2
0kl
l = 2n
etc...
En
definitiva, que mediante la observación del
patrón de
difracción de los cristales, y en concreto tras el estudio
de la posible existencia de reglas de extinción
sistemática, como las mostradas más arriba, se
puede concluir la presencia de elementos de simetría del
tipo reseñado: ejes
helicoidales y planos
de deslizamiento, y
en su
caso, la existencia de redes
centradas
(no-primitivas), lo cual supone una ayuda inestimable para la
determinación del Grupo Espacial del cristal.
EL
CENTRO DE SIMETRÍA
Como se
comenta al principio, sólo existe una
indeterminación, y es la del centro de simetría, tal como se deduce de la ley de
Friedel. Sin embargo, hay situaciones en las cuales la presencia de
este elemento de repetición resulta indudable como
consecuencia de la combinación de otros elementos de
simetría cuya existencia es patente a través de
las extinciones sistemáticas, tal como es el caso de uno de
los Grupos Espaciales más frecuentes, el P21/c,
en el cual coexisten ejes helicoidales paralelos al eje b
y planos de deslizamiento perpendiculares al eje b:
Los elementos de
simetría que
se muestran en la figura de la izquierda, tales como los ejes
helicoidales paralelos a b,
y los planos de deslizamiento, perpendiculares a ese mismo eje (líneas de puntos), provocan, respectivamente, que las
reflexiones existentes son las que cumplen las condiciones:
0k0 k =
2n ---> 21
h0l l = 2n
---> c
Los círculos de la figura de la izquierda, que
representan por ejemplo a átomos, se repiten por los
mencionados operadores, y si el lector observa con detenimiento dichas
repeticiones,
concluirá que dichas operaciones, combinadas, provocan que
en
los nudos de la celdilla (y a la mitad entre cada dos nudos) se generen
centros de simetría (pequeños círculos
de la
figura de la derecha), y
por ello el Grupo Espacial P21/c
es centrosimétrico.
Sin embargo, en otros casos, para poder concluir la
presencia o ausencia del centro de
simetría.
hay que
recurrir a:
- medidas
físicas
(efectos piezoeléctrico ó
piroeléctrico)
- test
estadísticos de
distribución de intensidades
- propia
resolución
estructural
Por
cierto, el lector se habrá dado cuenta también
del hecho de que si bien
la celdilla repite las cosas tras aplicar traslaciones completas de los
ejes de la celdilla, los elementos de simetría se repiten a
sí mismos a
la mitad de las translaciones de los ejes de la celdilla.
Pero volvamos
al punto de partida...
Tabla de
contenido
