6.
Difracción experimental
En el
contexto de este capítulo Vd será invitado
también a visitar estos apartados...
Independientemente de las grandísimas novedades que han
ocurrido para la generación de los rayos X,
las técnicas usadas para medir los ángulos y la
intensidad de los haces de difracción también han
evolucionado a lo
largo del tiempo. En el primer experimento de difracción,
Friedrich y Knipping (1912) usaron una película sensible a
los rayos X, pero incluso en el mismo año, Bragg
usó
una
cámara de ionización montada sobre un brazo
rotatorio
que, en general, determinaba con más precisión
los
ángulos y las intensidades de difracción. Sin
embargo, la
película representó la ventaja de poder
impresionar muchos
haces
difractados a la vez, y así durante
los primeros
años
de la Cristalografía estructural (desde 1920 hasta 1970) se
hizo
uso extensivo de los métodos fotográficos, y
entre ellos
se deben destacar los métodos de Laue, Weissenberg,
precesión
y oscilación.
A partir de mediados de la década de 1970, los
métodos fotográficos fueron paulatinamente
reemplazados por métodos
goniométricos acoplados
a detectores puntuales y posteriormente éstos
últimos han sido reemplazados por detectores de área.
Método
de Laue
En sus primeros
experimentos,
Max
von Laue (1879-1960) (Premio Nobel de Física en
1914) usó
radiación contínua (con todas las longitudes de
onda
posibles)
incidiendo sobre un cristal estacionario. De este modo, el cristal
generaba
un conjunto de haces que representan la simetría interna del
cristal.
En estas condiciones, y teniendo en cuenta la ley
de Bragg, las constantes del experimento son los
espaciados d
y
la posición del cristal respecto al haz incidente, y las
variables
son la longitud de onda λ
y el número entero n:
n
λ = 2
dhkl sen
θnh,nk,nl
Por lo tanto, para un mismo
espaciado d,
el patrón de difracción contendrá los diferentes haces difractados que se
corresponderán con el primer orden de
difracción (n=1)
para esa longitud de
onda (λ),
con el segundo orden (n=2),
que corresponderá a la longitud de onda mitad (λ/2), con el tercer orden (n=3),
que corresponderá a la longitud de onda λ/3, y así sucesivamente. Por lo
tanto, el diagrama de Laue es simplemente una
proyección
estereográfica de los planos del cristal. El
lector interesado puede también visitar la
simulación Java que se ofrece a través de este
enlace.
Diagrama
de Laue de un cristal
Hay dos
geometrías
diferentes en los diagramas de Laue, dependiendo de la
posición del cristal respecto
de
la
placa fotográfica, transmisión o
reflexión:
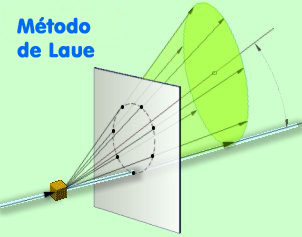
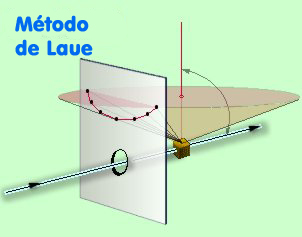
Izquierda: Método
de Laue en modo transmisión
Derecha: Método
de Laue en modo reflexión
Método
de Weissenberg
El
método de
Weissenberg
está basado en la cámara del mismo nombre,
desarrollada
en 1924 por el científico austriaco Karl
Weissenberg (1893-1976).
La influencia de K. Weissenberg en
la metodología fotográfica de
difracción puede consultarse en dos magníficos
artículos que
hace algunos años ofreció la Sociedad
Británica de Reología: "Weissenberg’s
Influence on Crystallography"
(de H. Lipson) (usar
este enlace en caso de problemas) y
"Karl
Weissenberg and the development of X-ray crystallography"
(de M.J. Buerger).
La cámara consta de un cilindro
metálico que
contiene
en su interior una película fotográfica sensible
a los
rayos
X. El cristal se monta sobre un eje coaxial con dicho cilindro y se
hace
girar según el modelo
de Ewald, de tal modo
que los puntos recíprocos
que
intersectan
la superficie de la esfera de Ewald son los responsables de los haces
de
difracción.
Estos haces generan ennegrecimientos (manchas)
sobre
la película fotográfica que, cuando se extrae del
cilindro
metálico, tiene la apariencia que se muestra más
abajo.
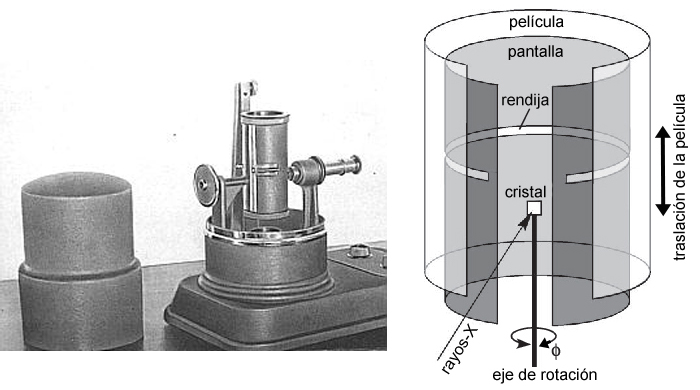Cámara
desarrollada por Karl Weissenberg en 1924
Esquema
y ejemplo de de una cámara tipo Weissenberg, usada en los
laboratorios de
Cristalografía
hasta aproximadamente 1975
El
tipo de diagramas
Weissenberg
que se obtienen, según el modo descrito, se denominan de rotación
o de
oscilación,
dependiendo
de que el giro del cristal sea completo (360º), o parcial
(aprox. 20º),
respectivamente, manteniendo inmóvil la película
fotográfica. Los diagramas de oscilación se utilizan
para centrar el cristal, es decir, para conseguir que el eje
de
giro del cristal coincida exactamante con un eje directo, lo que
equivale a decir que los planos recíprocos (que por
construcción geométrica son perpendiculares a
dicho eje
directo) generan manchas alineadas en la película
fotográfica. Una vez conseguido el centraje, los diagramas
de
rotación completa se utilizan para evaluar el valor del eje
directo del cristal, que coincide con la separación entre
las
líneas de manchas del diagrama.
Esquema
que explica la producción de un diagrama de Weissenberg del
tipo
rotación-oscilación
Tal como muestra
el esquema
de arriba, cada línea horizontal de puntos representa la
proyección sobre la placa fotográfica de un plano
recíproco perpendicular al eje de giro. La figura de la
izquierda muestra el
aspecto real de un diagrama de Weissenberg de tipo
rotación-oscilación. La distancia entre las
líneas de puntos
horizontales proporciona información sobre el periodo de
repetición del
cristal en la dirección vertical de la foto.
Tal como se ha dicho, en
la práctica, este tipo de diagramas se utilizaban para
centrar
los
cristales en la cámara de Weissenberg, es decir, para
conseguir que el
eje
de
giro del cristal fuera perpendicular a los planos
recíprocos,
representados aquí por las alineaciones de puntos que se
muestran.
El montaje del
cristal
debe ser tal que su eje de giro coincida con un eje directo de la
celdilla
elemental. De ese modo (por definición de la red
recíproca)
existirán planos recíprocos perpendiculares a
dicho eje. Los puntos recíprocos (que están sobre
dichos
planos reciprocos) giran solidariamente con el giro del cristal y
(después de pasar por la superficie de la esfera
de Ewald)
producen haces difractados, que dispuestos en forma de conos, chocan
contra la película cilíndrica y posteriormente
aparecen
como alineaciones horizontales de manchas de
difracción, tal como se observa en la placa
fotográfica.
Es
indudable que con
este tipo de diagramas se consigue información sobre los
períodos
de repetición de la red directa, ya que la
separación
entre
las líneas que contienen las manchas de
difracción es
proporcional
a la distancia entre planos de puntos recíprocos. Sin
embargo, cada
plano
recíproco (dos dimensiones) en el diagrama queda
representado sobre una línea
(una
dimensión)
de manchas de la película, dando lugar a solapamiento entre
manchas.
Este problema
quedó
resuelto cuando a las cámaras se les
añadió la
libertad
de traslación del cilindro, en la dirección
paralela a su
eje, acoplada al giro del cristal y seleccionando mediante dos
cilindros
internos el cono de difracción que origina uno solo de los
planos
recíprocos. De este modo, un plano recíproco (dos
dimensiones)
quedaría impresionado en toda la superficie de la placa
fotográfica
(dos dimensiones), evitando con ello el posible solapamiento entre
manchas.
Sin embargo, como consecuencia de la traslación en
vaivén
de la cámara durante el giro del cristal, se
origina una
deformación en la distribución de las manchas
(intesidades de difracción).
El
aspecto de un diagrama de este tipo, con la deformación
geométrica
que
se produce del plano
recíproco, se
muestra
en la figura de abajo. En estas condiciones, y teniendo en cuenta dicha
deformación, es posible medir aisladamente cada haz de
difracción. Y modificando adecuadamente la
posición de la
rendija que permite la salida de los conos de difracción, se
pueden recoger todos los
planos
recíprocos del cristal.
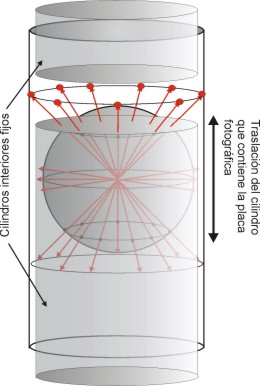
Izquierda:
Detalle
de la cámara de Weissenberg para separar un cono de haces
difractados
mediante dos cilindros internos que dejan una rendija. El cilindro
exterior, conteniendo una película fotográfica,
se traslada al mismo tiempo que el cristal gira,
distribuyéndose
las manchas de difracción, que antes estaban en una
línea,
sobre toda la placa fotográfica.
Derecha:
Diagrama
de Weissenberg del plano recíproco hk2 del metaborato de
cobre.
Método
de precesión
El
método de
precesión
fué desarrollado por Martin
J. Buerger (1903-1986), a principios de la
década
de 1940, como alternativa muy ingeniosa para poder impresionar placas
fotográficas
de planos recíprocos sin distorsionar.
Al igual que el
método
de Weissenberg, se trata de un método en el que cristal se
mueve,
pero el movimiento del cristal (y como consecuencia el de los planos
recíprocos
solidarios) es como el de precesión de los planetas, de
ahí
su nombre. La película fotográfica se coloca
sobre un
soporte
plano y se mueve solidariamente con el cristal.
El cristal
debe
orientarse
de tal modo que el plano recíproco que se desee recoger sea
perpendicular
al haz directo de los rayos X, es decir, que un eje directo coincida
con
la dirección de los rayos X incidentes.
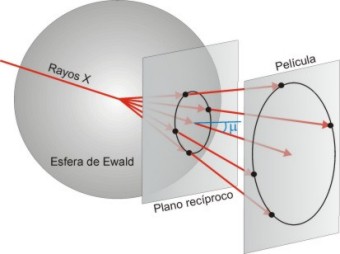Dos
visiones esquemáticas del principio en el que se basa la
cámara
de precesión. El ángulo μ
es
el ángulo de
precesión
del plano recíproco seleccionado del cristal y de la
película fotográfica, que se mantiene paralela al
plano
recíproco
y solidaria en movimientos al cristal.
La cámara
diseñada
para tal
efecto y el aspecto de
un diagrama de difracción de una muestra
inorgánica se
muestran
en las figuras de abajo.
Izquierda: Esquema
y aspecto de una cámara de precesión
Derecha:
Diagrama
de precesión de una perovskita, con simetría
cúbicaEste
tipo de diagramas
son
mucho más simples de interpretar que los de Weissenberg, ya
que
muestran el aspecto de un plano recíproco sin
distorsión.
La separación de un plano recíproco determinado
se
consigue
mediante el uso de pantallas (figura de arriba) que seleccionan los
haces
difractados de dicho plano. Del mismo modo a como ocurre en el caso de
Weissenberg, se pueden medir las distancias recíprocas y las
intensidades
de difracción. Sin embargo, aquí es mucho
más
facil
observar los elementos de simetría del espacio
recíproco.
La desventaja del
método de
precesión es
consecuencia de
que la película es plana en lugar de cilíndrica,
y el
ángulo
sólido explorado es menor.
Este método
se
ha usado con éxito durante muchos años, incluso
para el
caso
de macromoléculas como las proteínas:
Izquierda:
Diagrama
de precesión de un cristal de lisozima en el que
fácilmente
se distingue un eje de simetría cuaternario perpendicular al
diagrama.
Debido a que los ejes de la celdilla elemental son grandes, la
separación
entre los puntos recíprocos es pequeña
Derecha: Diagrama
de precesión de un compuesto orgánico sencillo,
en el que
se observa simetría
mm.Obsérvese que la
separación
entre los puntos recíprocos es mucho mayor (menores ejes
reticulares
directos) que en el caso de las proteínas (mayores ejes
reticulares
directos)
Método
de oscilación
Originalmente,
los
métodos
de monocristal, con giro amplio de la muestra, como los mencionados
anteriormente,
se impusieron por su facilidad de interpretación. Sin
embargo,
cuando
se llegó a experimentar con redes directas con periodos de
traslación grandes, es
decir,
con redes recíprocas
con periodos de traslación pequeños (puntos
recíprocos muy cercanos), los tiempos de recogida se
disparaban
y por lo
tanto
se
recurrió al método de oscilación con
ángulos
pequeños. Esta
metodología permitía recoger
varios niveles
recíprocos
a la vez sobre cada posición del cristal. Repitiendo estos
diagramas,
a distintas posiciones de partida del cristal, se conseguían
obtener
suficientes datos en un tiempo razonable. La geometría de
recogida
está descrita en las figuras que vienen a
continuación.
Hoy en día,
con
generadores de ánodo rotatorio o sincrotrones, y detectores
de
área
(image
plate ò CCD,
ver más abajo), que aumentan la intensidad de los
máximos
de difracción y reducen los tiempos de recogida con gran
fiabilidad,
se ha impuesto este método para los estudios de
macromoléculas,
en particular de proteínas.
Esquema
de la geometría de las condiciones de máximo de
difracción
en el método de oscilación. El cristal, y por
tanto la
red
recíproca, están oscilando un pequeño
ángulo
alrededor de un eje perpendicular al plano de la figura y que pasa por
el centro. En la figura de la derecha, el área que pasa por
condición
de máximo de difracción está denotada
por el
área
amarillenta, delimitada por la esfera de Ewald (de radio 2.sen 90/λ)
en los dos extremos de oscilación de la red, y la esfera de
resolución
máxima (de radio 2.sen θmax/λ)
que se puede alcanzar con la radiación empleada y con el
detector
que se haya usado.
Cuando la red recíproca oscila
un pequeño ángulo, alrededor del eje de giro,
pequeñas zonas de los diferentes niveles de la red
recíproca entran en contacto con la esfera de Ewald,
alcanzando las condiciones de máximo de
difracción. De este modo, sobre la pantalla del detector, la
geometría de oscilación produce
máximos de difracción procedentes de diferentes
niveles de la red recíproca y formando lúnulas
sobre el diagrama (figura de la derecha)
Goniometría
de cuatro círculos
La
introducción
de los computadores digitales a finales de la década de
1970,
permitió
el diseño de los llamados
difractómetros
automáticos de cuatro círculos.
Estos equipos,
disponen de un sistema goniométrico, con una
mecánica muy
precisa, que mediante tres giros permite colocar el cristal en
cualquier
orientación del espacio, provocando así que se
cumplan
los
requerimientos de la construcción de Ewald
para que se
produzca
la difracción. En estas condiciones, un cuarto eje de giro,
que
sustenta el detector electrónico se coloca en condiciones de
recoger
el haz difractado. Todos estos movimientos se pueden programar para que
se realicen de un modo automático, con una mínima
intervención
del operador.
Entre este tipo de
goniómetros
se pueden distinguir dos geometrías goniométricas
que se
han usado con excelente éxito durante muchos
años. En el
goniómetro de geometría
Euleriana
(ver figura de abajo) el cristal se orienta mediante los tres
ángulos
de Euler, Φ
que
representa el giro sobre el eje de la cabeza
goniométrica, χ
que
le permite el balanceo sobre el círculo cerrado, y ω
que
permite el giro total del goniómetro. El cuarto
círculo
lo
representa el giro del detector,
2θ.
Esta
geometría, presenta la ventaja de la estabilidad
mecánica,
pero por contra restringe la accesibilidad al cristal para equipos
externos
de baja o alta temperatura.
Izquierda: Esquema
y aspecto de un goniómetro de cuatro círculos con
geometría
Euleriana
Derecha: Rotaciones en un
goniómetro de cuatro círculos con
geometría
Euleriana
La geometría
alternativa
a la Euleriana es la denominada
geometría
Kappa que no dispone de un círculo
cerrado
equivalente
al χ.
En
su lugar, su función la cumplen los llamados ejes κ
(kappa) y ωκ,
de tal modo que con una combinación de ambos se pueden
obtener χ
eulerianos
en el intervalo de -90 a +90º. La ventaja principal de esta
geometría
es la amplia accesiblidad al cristal. Los ángulos Φ
y
2θ
son
idénticos al los de la geometría euleriana:
Esquema
y aspecto de un goniómetro de cuatro círculos con
geometría
Kappa.
Tanto en la
geometría
Euleriana
como Kappa,
el sistema de
detección
ampliamente usado durante muchos años es el denominado
"puntual",
en el sentido de que la detección de cada haz difractado
(reflexión)
se realiza de modo individual, necesitando cambiar, de modo
automático
y programado, los cuatro valores angulares del goniómetro
para
cada
haz difractado. Los tiempos de medida en estos equipos suele ser del
orden
de 1 minuto por reflexión.
Uno de los
detectores
más ampliamente usados ha sido el denominado
detector
de centelleo, cuyo esquema de funcionamiento es el siguiente:
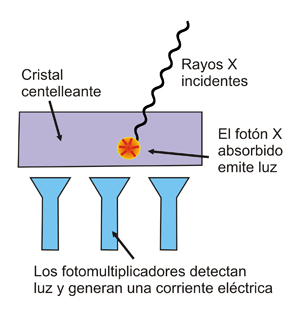
Esquema de un detector de centelleo
Detectores
de área
Como alternativa a
los
detectores "puntuales", el desarrollo de la tecnología
electrónica
ha dado lugar a la aparición de los denominados detectores
de área, que permiten la
detección de muchos
haces
de difracción simultáneamente, ahorrando con ello
tiempo
en el experimento. Esta tecnología es de especial utilidad
para
el caso de las proteínas y en general de cualquier material
que
pueda deteriorarse durante su exposición a los rayos X, ya
que
la
detección de cada una de las imágenes que se
recogen (con
varios cientos o miles de reflexiones) se hace en un tiempo
mínimo,
del orden de los segundos.
Uno de los
detectores
de área mas comunmente usado se basa en los denominados CCD's
(del inglés
Charge
Coupled Device) cuyo esquema se muestra
a continuación:
Esquema
de un CCD con indicación de sus componentes principales.El
conversor
de rayos X (D en la figura) es un material sensible, del tipo P, GdOS,
etc., que es capaz de convertir los rayos en pulsos
eléctricos.
Los CCD's operan a una gran velocidad de conversión, aunque
su
desventaja
es la de operar a muy bajas temperaturas (del orden de -70 ºC).
Los detectores del
tipo
CCD
se instalan normalmente sobre equipos goniométricos con
geometría
Kappa
(κ)
y por su rapidez, su uso está ampliamente extendido en el
ámbito
de la Cristalografía de proteínas, asociados a generadores
de ánodo rotatorio o en las grandes instalaciones
de sincrotrón.
Izquierda: Goniómetro
de geometría Kappa con detector tipo CCD. (Imagen
tomada de Bruker-AXS)
Derecha: Detalle
del montaje de un goniómetro con geometría Kappa
(aunque
con ángulo κ
fijo)
Otro tipo de
detectores
de amplio uso hoy en día, especialmente en la
Cristalografía
de proteínas es el llamado Image
Plate
Scanner que generalmente se montan sobre un
goniómetro
relativamente rudimentario, cuya única libertad de giro
corresponde
a la del cristal sobre su eje de montaje. El detector propiamente dicho
es una placa circular de material sensible a los rayos X que se
interpreta,
después de la exposición, mediante un laser capaz
de
digitalizar
las intensidades.
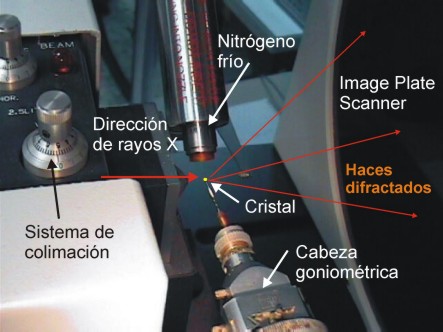Izquierda: Image
Plate Scanner. (Imagen
tomada de Marxperts)
Derecha: Detalle
de un detector del tipo Image Plate Scanner
La
tecnología más
moderna implica el uso de detectores de área basados en la
denominada tecnología CMOS
(complementary
metal-oxide
semiconductor:
semiconductor de óxido metálico
complementario)
que
permite un tiempo de lectura muy corto, lo que conduce a un aumento
considerable de la tasa de obtención de imágenes
de
difracción durante el proceso de recogida de datos.
Detectores de área
XALOC,
vista del equipo para cristalografía de
macromoléculas
(izquierda) instalado en el sincrotrón
español ALBA
(derecha)
En definitiva, la
recogida de un patrón de
difracción completo consiste en la
obtención de multitud de
imágenes
como la que se muestra más abajo, y que posteriormente
serán
analizadas
para obtener la métrica del cristal (constantes
reticulares), su simetría (grupo espacial) e intensidades
de difracción. Este proceso se explica con un poco
más de detalle en otro apartado de este capítulo.
Izquierda:
Aspecto
de una de las imágenes de difracción, del tipo
oscilación,
de una proteína recogida en un Image Plate Scanner. Durante
la
exposición
de cada una de estas imágenes (unos 5-10 minutos con un
generador
de ánodo rotatorio, o de varios segundos en una
instalación
de sincrotrón) el cristal gira aproximadamente 0.5º
y la
lectura
de la imagen dura unos 15 segundos. Este
podría ser también el aspecto de una imagen de
difracción
recogida en un detector de tipo CCD, aunque en este caso probablemente
la duración de la exposición habría
sido algo
más
corta.
Derecha:
Colección
de imágenes de difracción consecutivas obtenidas
en
un detector de tipo Image Plate Scanner o CCD. Con el paso del tiempo aparecen dos
anillos oscuros,
concéntricos con la imagen, que corresponden a la suma de
infinitos puntos recíprocos de dos de los órdenes
de
difracción de microcristales de hielo que, de forma
desorientada, se forman por algún defecto del crioprotector
o de
cierta humedad que acompaña al nitrógeno frio que
baña al cristal.
Imágenes
tomadas de Janet
Smith Lab. Observe
también este ejemplo
suministrado por Aritra Pal y Georg Sheldrick
En todas estas
metodologías
(excepto en el caso del método de Laue), la
radiación que se utiliza suele ser monocromática
(o casi), es decir, que es una radiación X que contiene
exclusivamente
(o casi) una única longitud de onda, y para ello se suelen
utilizar los
llamados monocromadores,
compuestos por un sistema de cristales que, basándose en la ley
de Bragg, son capaces de "filtrar" (por el propio proceso de
difracción) la radiación policromática
y "dejar pasar"
sólo una de las longitudes de onda (color), tal como se
muestra en la
figura de abajo:
Esquema
de un monocromador. Una radiación policromática
(blanca) que llega por
abajo a la izquierda, y se "refleja" de acuerdo con la ley
de Bragg,
en distintas orientaciones del cristal, para dar lugar a una
radiación
monocromática que se vuelve a reflejar ("filtrar") en el
segundo
cristal. Imagen tomada del ESRF.
En
la actualidad, en
los laboratorios de Cristalografía, o incluso en las nuevas
líneas de radiación
sincrotrón, los
monocromadores tradicionales están siendo reemplazados por
nuevos componentes ópticos que han demostrado una eficacia
superior a los primeros. Estos componentes reciben el nombre
genérico de "espejos" y pueden estar basados en los
fenómenos de:
- reflexión
total (espejos, capilares y guías de onda),
- refracción
(lentes de refracción) y
- difracción
(cristales, basados en la técnica del monocromador, y
materiales en multicapas, etc.)
Puede
resultar también muy
ilustrativo observar este esquema animado de mas abajo, mostrando el
camino que
recorre cada fotón de rayos X en un determinado sistema de
difracción actual:
- el
fotón sale de la fuente
en donde se producen los rayos X,
- pasa por los
diferentes elementos ópticos que lo encauzan por el camino
adecuado (espejos, rendijas y colimadores),
- incide
sobre el cristal único, y
- finalmente
genera los efectos de difracción sobre un detector
Con objeto
de obtener el mejor (y mayor) conjunto
de datos de la red recíproca se debe usar igualmente un
equipo de
enfriamiento de la muestra, que proporciona una corriente de
nitrógeno
seco a temperatura de unos 100 K (es decir aproximadamente a -170
ºC). De
este modo, los cristales (y especialmente los de
macromoléculas) son
más estables y resisten mejor la
radiación X. Con ello se consigue, además,
reducir los factores de
vibración térmica de los
átomos y por lo tanto facilitando su localización
Para
montar los cristales en el
flujo de nitrógeno frío suelen usarse
unos
pequeños lazos que sirven para "pescar" el cristal en una
matriz
que sea transparente a los rayos X.
Esto es especialmente importante en
el caso de los cristales de proteína, en los que dicha
matriz es
un crio-protector (anti-congelante) que se dispersa por los canales
interiores del cristal y reemplaza las moléculas de agua por
las
del crio-protector; de no hacerse de este modo, la
congelación del agua interna provocaría la
ruptura del cristal.
Izquierda: Detalle
del montaje de un cristal mediante un lazo relleno de una matriz
anticongelante
Derecha: Comprobación
de la situación del cristal en el centro óptico goniométrico.
Vídeo cortesía
de Ed
Berry
En
cualquiera de los casos, el cristal debe de quedar situado en el centro
óptico del goniómetro, por el que
tambíén
deberá pasar el haz de rayos X. De este modo, cuando el
cristal gire,
deberá hacerlo
siempre centrado sobre dicho punto, con lo que en cualquiera de sus
posiciones estará bañado por el haz de rayos
X.
Sistema
de
crioprotección montado en un goniómetro
La
corriente de
nitrógeno a -170 ºC llega por el conducto superior
y
enfría el cristal montado sobre una cabeza
goniométrica
que gira. El
colimador del haz de rayos X apunta hacia el cristal desde la
izquierda de la imagen.
Obsérvese el ligero vapor que genera la corriente
fría de
nitrógeno cuando se mezcla con el aire húmedo del
ambiente.
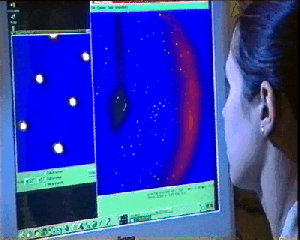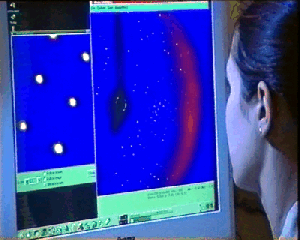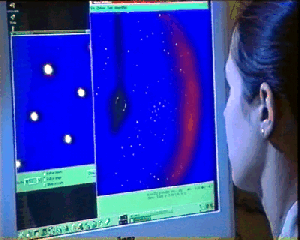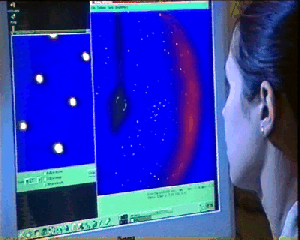Analizando visualmente la calidad del
patrón de difracción
En
resumen, todos estos
métodos
permiten obtener una colección de datos, formados por tres
índices
de Miller y una intensidad para cada uno de los máximos de
difracción
medidos. Con ello, se debe poder conseguir medir la
mayor parte posible de la red
recíproca, ponderada con intensidades, es
decir, el patrón
de
difracción completo de un monocristal de la muestra a
estudiar.
Por lo tanto, es necesario evaluar
totalmente el
patrón de difracción, y ello implica la
medida de su geometría y de sus intensidades.
Más
adelante veremos que toda la información
extraída de
la única observación
experimental disponible (patrón de difracción, o
espacio recípoco) es
imprescindible para poder determinar la arquitectura del
interior del cristal, es decir, las posiciones de los átomos
que lo constituyen. Pero eso
será
objeto de otro capítulo ...
