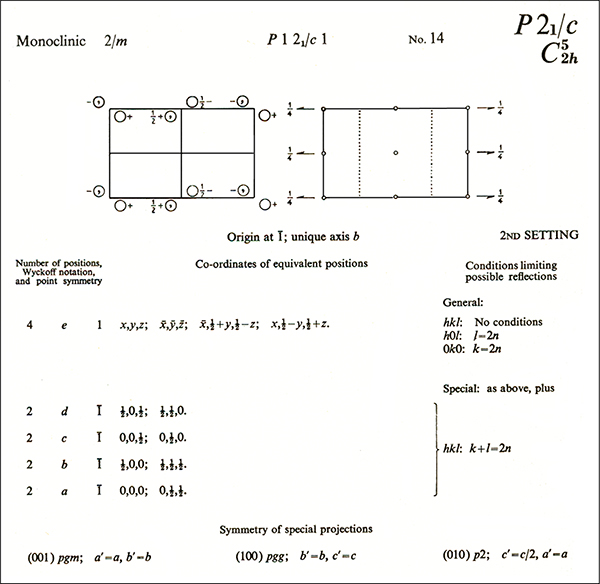
where, if we forget the
commas and the
colon, it becomes:
AMANAPLANACANALPANAMA
which
can be read from right to left with
exactly the same meaning as above.
It is a case similar to the "palindromic" numbers (232 or
679976).
There
are many links in which the reader
can find information on the concept of symmetry and we have selected
some of them: symmetry
and shape of space,
some others in the context with
decorative patterns, or
in the context
of minerals. There is
even an international
society for the study of symmetry.
The essential knowledge on crystal morphology, symmetry elements and
their combination to generate repetitive objects in space, were well
established between the 17th and 19th Centuries, as
stated
elsewhere in these pages...
Specifically,
in finite objects, there are a number of operations (
elements
of symmetry) describing repetitions. In the
wall-drawing (shown above) we find
translational
operations (the motif is repeated by translation). The
repetition of the petals in the flowers show us
rotational
operations (the motif is repeated by rotation) around a
symmetry
axis (or
rotation
axis). And, although not exactly, the symmetry shown in
the
phrase or in the
music fragment (shown above), lead us to consider other symmetry
operations known as
symmetry
planes (
reflection
planes, or
mirror
planes); the same operation that occurs when
you look into a mirror. Similarly, for
example, if we look at the relationship between the three-dimensional
objects in some of the pictures shown below, we will discover a new
element of
symmetry called
center
of symmetry (or
inversion
center), which is an imaginary
point between objects (or inside the object) as shown
in some drawings below.
Generally speaking,
and taking into
account that pure translational operations are not strictly considered
as
symmetry operations, we can say that
finite objects can contain themselves, or may be repeated (excluding
translation) by the
following symmetry elements:
- The identity
operation is the simplest symmetry element of all
-- it does nothing! But it is important because all objects at the very
least
have the identity element, and there are many objects that have no
other
symmetry elements.
- The reflection
is the symmetry operation that occurs when we put an
object in front of a mirror. The image is found perpendicular to the
reflection plane and equidistant from that plane, on the opposite side
of the plane. The resulting object can be distinguishable or indistinguishable
from the original, normally distinguishable,
as they
cannot be superimposed. If the resulting object is indistinguishable
from the original, is because the reflection plane is passing through
the object.
- The inversion
operation occurs through a single point called the inversion
center. Each part of the object is moved along a
straight line through the inversion center to a point at an equal
distance from the inversion center. The resulting object can be distinguishable or indistinguishable
from the original, normally distinguishable,
as they cannot be superimposed. If the resulting object is indistinguishable
from the original, is because the inversion center is inside the object.
- The rotation
operations (both proper
and improper)
occur with respect
to a line called rotation axis. a)
A proper
rotation is performed by
rotating the object 360°/n,
where n
is the order of the axis. The
resulting rotated object is always indistinguishable from the original.
b)
An improper
rotation
is performed by rotating the object 360°/n
followed by a reflection through a plane perpendicular to the rotation
axis. The resulting object can be distinguishable
or indistinguishable
from the original, normally distinguishable, as they cannot be
superimposed. If the resulting object is indistinguishable
from the original, is because the improper rotation axis is passing
through the object.
In addition to the name of the
symmetry
elements, we use graphical and numerical symbols to
represent them. For
example, a rotation axis of order 2 (a binary axis) is represented by
the number 2,
and a reflection plane is represented by the letter m.

 Left: Polyhedron
showing a two-fold rotation
axis (2) passing
through
the centers of the top and bottom edges
Right: Polyhedron showing
a reflection plane (m) that
relates (as a mirror
does) the top to the bottom
Left: Polyhedron
showing a two-fold rotation
axis (2) passing
through
the centers of the top and bottom edges
Right: Polyhedron showing
a reflection plane (m) that
relates (as a mirror
does) the top to the bottomHands and molecular models related by a
twofold
axis (2) perpendicular to the drawing plane
Hands and molecular models related
through a mirror
plane (m) perpendicular to the drawing plane
Hands (left and right) related through a
center of symmetry

 Two objects related by a center of
symmetry and a polyhedron showing
a center of symmetry in its center
Two objects related by a center of
symmetry and a polyhedron showing
a center of symmetry in its center
The
association of elements of rotation with centers or planes of
symmetry generates new elements of symmetry called improper
rotations.
Right: Axis
of
improper rotation, shown vertically, in a crystal of urea. The
meaning of numerical triplets shown will be discussed in
another
chapter.
Combining
the rotation axes and the mirror planes with the characteristic
translations
of the crystals (which are shown below), new symmetry elements
appear, with some "sliding" components: screw
axes (or helicoidal
axes)
and glide
planes.
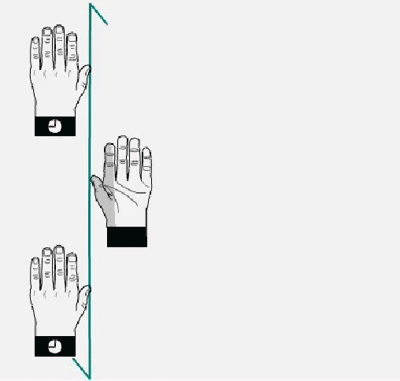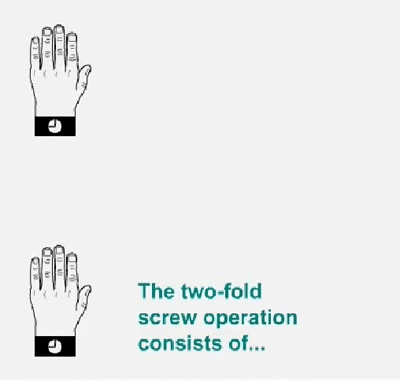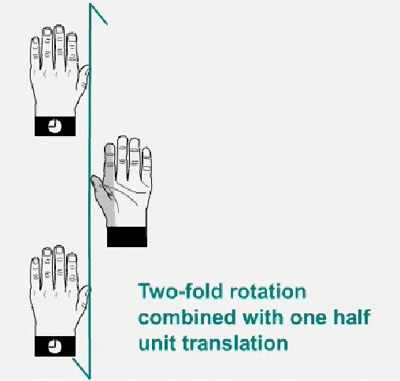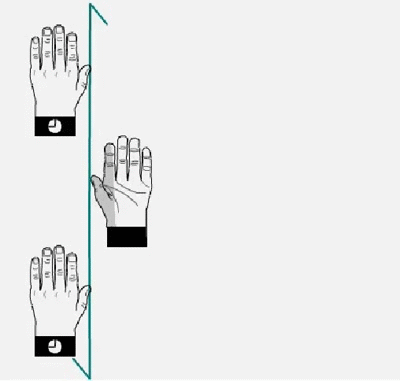
Twofold screw axis. A screw axis consists
of a rotation followed by a translation
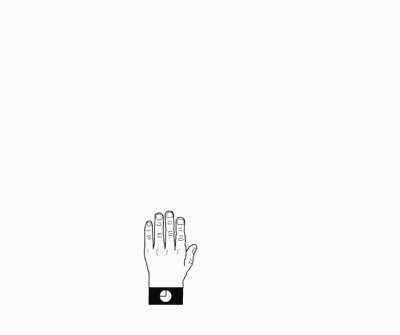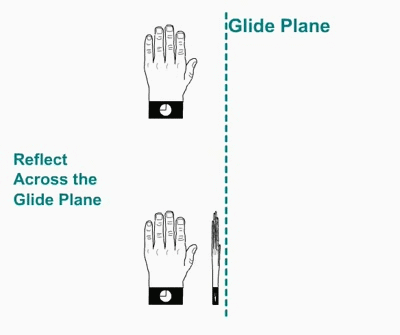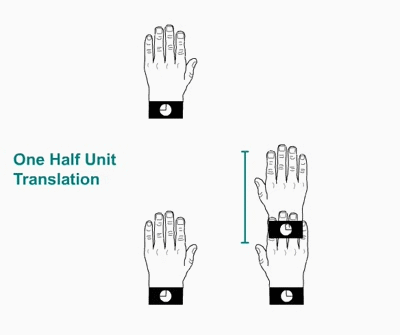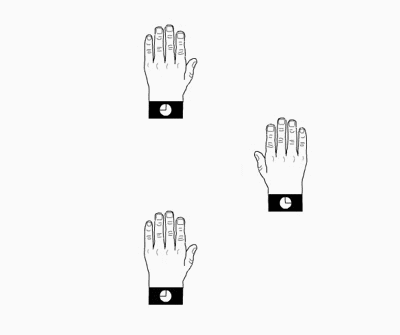
 Glide plane. A glide plane consists of a reflection
followed by a translation
Glide plane. A glide plane consists of a reflection
followed by a translation
Twofold
screw axis applied to a left hand. The hand rotates 180º and
moves
a half of the lattice translation in the direction of the screw axis,
and so on. Note that the hand always remains as a left hand.
Glide plane.applied to a left hand. The
left hand reflects on the
plane, generating a right hand that moves a half of the lattice
translation in the direction of the glide operation.
The symmetry
elements of types
center
or
mirror
plane
relate
objects in a peculiar way; the same way that our two hands
are related one to the other: they are not superimposable.
Objects
which in themselves do not contain any of these symmetry
elements (center or plane) are called
chiral
and their repetition through these elements
(center or plane)
produce objects that are called
enantiomers
with respect to the original ones. The mirror image of one of our hands
is the enantiomer of the one we put in front of the mirror.
The
mirror image of either of our hands is the enantiomer of the other
hand.
They are objects not superimposable and as they do not contain
(in themselves) symmetry centers or symmetry planes, are
called chiral objects.
Chiral molecules have different
properties than their enantiomers and
so it is important that we are able to differentiate them. The
correct determination of the absolute
configuration or absolute
structure of a molecule (differentiation between
enantiomers)
can be done in a secure manner through X-ray
diffraction
only, but this will be explained in another
chapter
Molecular
chirality is critically important in
both chemistry and biology for several reasons, particularly due to how
it influences molecular interactions and the behavior of substances.
Here's why it's so significant:
- Biological
Interactions:
- Enzyme-Substrate Specificity, Many biological processes
rely on
the specific recognition of molecules by enzymes, receptors, and other
biomolecules. Enzymes, for example, often recognize and catalyze
reactions involving only one enantiomer (one of the two mirror-image
forms of a chiral molecule). If the enantiomer is incorrect, the
reaction may not proceed or could lead to harmful products.
- Chirality in Metabolism. Our bodies are highly selective in
how
they use chiral compounds. For example, the amino acids in proteins are
almost exclusively left-handed (L-amino acids), while sugars in nucleic
acids are right-handed (D-sugars). This specificity ensures the correct
folding and function of proteins, enzymes, and nucleic acids.
- Pharmacology and Drug Design:
- Different Biological
Effects. A chiral
molecule's two enantiomers can have drastically different effects in
the body. One enantiomer of a drug might be effective in treating a
disease, while the other could be less effective, inactive, or even
toxic. A well-known example is thalidomide, a drug that caused birth
defects because one enantiomer was beneficial, but the other caused
harm.
- Pharmacokinetics and
Pharmacodynamics.
The body's absorption, distribution, metabolism, and excretion (ADME)
of drugs can differ for each enantiomer. In some cases, one enantiomer
might be metabolized more quickly, or might interact with a different
set of receptors, which affects the overall efficacy and safety of a
drug.
- Optical Activity:
- Light Polarization:
Chiral molecules can
rotate the plane of polarized light. This property is important in many
analytical techniques, including polarimetry, where the degree of
rotation is used to determine the concentration of a chiral substance
in a solution. The direction of rotation (clockwise or
counterclockwise) can also distinguish between the two enantiomers of a
compound.
- Chemical Synthesis:
- Stereoselectivity in
Synthesis. In
chemical synthesis, controlling chirality is essential for creating
molecules with the desired activity. Often, one enantiomer of a
molecule is needed for a particular function, and selective synthesis
methods must be employed to ensure that only one enantiomer is produced
in high yield.
- Chiral Catalysis.
Certain catalysts are
used in the synthesis of chiral molecules to control the formation of
one enantiomer over the other. This is important in producing pure
pharmaceuticals, agrochemicals, and other specialty chemicals.
- Molecular Recognition and Binding:
- Receptor Binding. In
both chemical and
biological systems, chiral molecules can bind to specific receptors or
proteins in a manner similar to a key fitting into a lock. If the
chirality is incorrect, the molecule may not fit the receptor properly,
preventing it from having the desired effect. This selectivity is
crucial for things like neurotransmitter function, immune responses,
and enzyme catalysis.
- Environmental and Ecological
Impact:
- Chirality in Nature:
Many natural
products, such as amino acids, sugars, and alkaloids, are chiral. The
chirality of these compounds is often essential for their biological
roles. For instance, the chirality of the molecules in the cell
membrane affects how cells communicate and interact with the
environment, which can influence cellular processes and organismal
behavior.
In conclusion, molecular
chirality is important because it governs how molecules interact with
biological systems, affects drug design and efficacy, and plays a
crucial role in many chemical reactions and synthetic processes. In the
world of living organisms, chirality is essential for proper
biochemical function, and in synthetic chemistry, it's crucial for
creating molecules with the desired properties and activities.
The interested reader should not forget to read the article written by
Istvan
Hargittai & Magdolna Hargittai, which can be found at this link.
Also regarding the chirality of crystals and of their building
units
(molecular or not), advanced readers should also consult the
article by Howard D. Flack to
be found through this link.
Thus, any finite object (such as a quartz crystal, a chair or a flower)
shows that certain parts of it are repeated by symmetry operations that
go through a point of the object. This set of symmetry operations is
known as a
symmetry
point group. The advanced reader has also the opportunity
to visit the nice work on
point
group symmetry elements offered through
these links:
Additionally, the reader can download (totally virus free!!!)
and run on his own computer
this
Java application that, as an introduction to the symmetry of the
polyhedra, that was developed by Gervais Chapuis and
Nicolas Schöni (École
Polytechnique Fédérale de Lausanne, Switzerland).
Symmetry in crystals
In crystals, the symmetry
axes (rotation axes) can only be
two-fold
(
2),
three-fold
(
3),
four-fold
(
4)
or
six-fold
(
6),
depending on the number of times (
order
of rotation) that
a motif can be repeated by a rotation operation, being transformed into
a new state indistinguishable from its starting state.
Thus, a rotation axis of order
3
(3-fold) produces
3
repetitions (copies) of the motif, one every 120 degrees (= 360/
3)
of rotation. If the reader wonders why only symmetry axes
of order
2,
3,
4
and
6
can occur in crystals, and not
5-,
7-fold,
etc., we recommend the
explanations given in another
section.
Improper
rotations
(rotations followed by reflection through a plane perpendicular to the
rotational axis) are designated by the order of rotation, with
a
bar above that number.
The
screw
axes (or
helicoidal axes, ie, symmetry axes involving rotation followed by a
translation along the axis) are represented by the order of rotation,
with an added subindex that
quantifies the translation along the axis. Thus, a screw axis of
type
62
means that in each of the six rotations an
associated translation occurs of
2/
6
of the axis of the elementary cell in that direction.
The mirror
planes are represented by the letter m.
The
glide
planes (mirror planes involving reflexion and a
translation parallel to the plane) are represented by the
letters
a,
b,
c,
n
or
d,
depending if the translation associated with the reflection is parallel
to the reticular translations (
a,
b,
c),
parallel to the diagonal of a reticular plane (
n),
or parallel to a diagonal of the unit cell (
d).
The letters and
numbers that are used to represent the symmetry
elements also have an equivalence with some graphic
symbols.
But in order to keep talking about symmetry in crystals, it is
necessary to introduce and remember the fundamental aspect that defines
crystals, which is the periodic repetition by translation of motifs
(atoms, molecules or ions). This repetition, which is illustrated in
two dimensions with gray circles in the figure below, is derived from
the mathematical concept of lattice that we will see more properly in another
chapter.

In
a
periodic and
repetitive set of
motifs (gray circles in the two-dimensional figure above) one can find
infinite basic units (unit
cells) vastly different in appearance and
specification, the repetition of which generates the same mathematical
lattice. Note that
all represented unit
cells delimited by black lines contain in total a single circle inside
them, since each vertex contains a certain fraction of a circle inside
the cell. These are called primitive
cells. However, the cell
delimited by red lines contains a total of two gray circles inside (one
corresponding to the vertices and a complete one in the center). This
type of unit cell is generically called non-primitive.
Periodic repetition, which is a characteristic of the internal
structure of crystals, is represented by a set of translations in the
three directions of space, so that crystals can be seen as the stacking
of the same block in three dimensions. Each block, of a
certain shape and size (but all of them being identical), is called a
unit
cell or
elementary
cell. Its size is determined by the length of its three
edges (
a, b, c)
and the angles between them (alpha, beta, gamma:
α,
β,
γ).
Stacking of unit cells forming an octahedral crystal and parameters
which characterize the shape and size of an elementary cell
(or unit cell)
As
mentioned above, all symmetry
elements passing
through a point of
a finite object, define the
total
symmetry of the object, which is known as the point
group symmetry
of the object. Obiously, the symmetry elements that imply any lattice
translations (glide planes and screw axes), are not point group
operations.
There are many symmetry
point groups,
but in crystals they must be consistent with the crystalline
periodicity (translational periodicity). Thus, in crystals,
only
rotations (symmetry axes) of order 2, 3, 4 and 6 are possible, that is,
only rotations of 180º (= 360/2), 120º (= 360/3),
90º (=
360/4) and 60º (= 360/6) are allowed. See also the crystallographic
restriction theorem.
Therefore, only 32 point
groups are allowed in the crystalline state of matter.
These 32
point groups are also known in Crystallography as the 32
crystal classes.
point group . crystal translational
periodicity = 32 crystal classes

The motif, represented by a single
brick, can also be represented by a lattice point. It shows
the point symmetry 2mm
The next three tables show animated drawings about the 32 crystal
classes, grouped in terms of the so called crystal
system (left column), a classification mode in
terms of minimal symmetry, as shown below.
Lluis Casas and Eugenia Estop, from the
Department of Geology of the University of Barcelona, offer 32
pdf files which, in an interactive way, allow very easily
playing with the 32 point groups through the symmetry of crystalline
solids.
Additionally, the reader can download and run on his own computer this
Java application that, as an introduction to the symmetry of the
polyhedra,
was developed by Gervais Chapuis and Nicolas Schöni
(École
Polytechnique Fédérale de Lausanne, Switzerland).
Alternatively, the interested
reader can interactively view some typical polyhedra of the 7 crystal
systems, through the Spanish
Gemological Institute.
Of
the 32
crystal
classes, only 11
contain the operator center
of symmetry, and these 11
centro-symmetric crystal classes are known as Laue
groups.
crystal
class . center
of symmetry = 11 Laue
groups
In
addition, the repetition modes by translation in
crystals must be compatible with the possible point groups
(the 32
crystal classes), and this is why we find only 14
types of translational lattices which are compatible with
the crystal classes. These types of lattices
(translational repetiton
modes) are known as the Bravais
lattices (you can see them here).
The translational symmetry of an ordered distribution of 3-dimensional
objects can be described by many types of lattices, but there is always
one of them more suited to the object, ie: the one that best
describes the symmetry of the object. As the lattices
themselves have their own distribution of symmetry elements,
we
must fit them to the symmetry elements of the structure.
crystal
translational periodicity . 32 crystal classes
= 14 Bravais
lattices

A
brick wall can be structured with many different types of
lattices, with different origins, and defining reticular
points representing the brick. But there is a lattice that is
more
appropriate to the symmetry of the brick and to the way the bricks
build the wall.
The
adequacy of a lattice to the
structure is illustrated in the two-dimensional examples
shown below. In all three cases two different lattices are
shown, one oblique and primitive and one rectangular and
centered. In
the first two cases, the rectangular lattices are the most
appropriate ones. However, the deformation of the
structure in the third example leads to metric relationships that make
that the
most appropriate lattice,
the oblique primitive, hexagonal in this case.

Adequacy of the lattice type to the
structure. The blue lattice is the best one in each case.
Finally, combining
the 32
crystal classes (crystallographic point groups) with the 14 Bravais
lattices,
we find up to 230 different ways to replicate a finite object (motif)
in 3-dimensional space. These 230
ways to repeat patterns in space,
which are compatible with the 32 crystal classes and with the 14
Bravais
lattices, are
called space
groups,
and represent the 230 different ways to fit the Bravais
lattices to the symmetry of the objects. The interested reader
should also consult the excellent
work on the symmetry elements present in the space groups,
offered by Margaret Kastner, Timathy Medlock and Kristy Brown
through this link of the Bucknell University.
32
crystal classes
+ 14 Bravais lattices
= 230 Space groups

A
wall of bricks showing the most appropriate lattice which best
represents both the brick and its symmetry. Note that in this case the
point symmetry of the brick and the point symmetry of the reticular
point are coincident. The space group, considering the
thickness of the brick, is Cmm2.
The
32 crystal
classes, the 14 Bravais lattices and the 230 space groups can
be
classified, according to their hosted minimum symmetry, into 7
crystal systems.
The minimum symmetry produces some restrictions in the metric values
(distances and angles) which describe the shape and size of the lattice.
32 classes, 14 lattices, 230 space groups
/ crystal symmetry
= 7 crystal systems
All
this is summarized in the following
table:
Crystal
classes
(* Laue) |
Compatible
crystal lattices
and their
symmetry |
Number
of
space groups |
Minimum
symmetry |
Metric
restrictions |
Crystal
system |
| 1
1 * |
P
1 |
2 |
1 or
1 |
none |
Triclinic |
| 2
m
2/m * |
P
C (I)
2/m |
13 |
One
2
or
2 |
α=γ=90
|
Monoclinic |
| 222
2mm
mmm * |
P
C (A,B) I
F
mmm |
59 |
Three 2
or 2 |
α=β=γ=90
|
Orthorhombic |
4
4 4/m *
422 4mm
42m
4/mmm * |
P
I
4/mmm |
68 |
One
4
or 4 |
a=b
α=β=γ=90
|
Tetragonal |
3
3
*
32 3m 3m
* |
P
(R)
3m
6/mmm |
25 |
One
3
or 3 |
a=b=c
α=β=γ
(or
Hexagonal)
|
Trigonal |
6
6
6m *
622 6mm
6m2
6/mmm * |
P
6/mmm |
27 |
One 6
or 6 |
a=b
α=β=90
γ=120 |
Hexagonal |
23
m3 *
432 43m
m3m * |
P
I
F
m3m |
36 |
Four 3
or 3 |
a=b=c
α=β=γ=90
|
Cubic |
Total:
32, 11 *
|
14
independent |
230 |
|
|
7 |
The 230 crystallographic space
groups are
listed and described in the International
Tables for X-ray Crystallography,
where they are classified according to point groups and
crystal systems. Chiral compounds that are prepared as a
single enantiomer (for
instance, biological molecules)
can crystallize in only a subset of 65 space groups, those that do not
have mirror and/or inversion symmetry operations.
A
composition of part of the information
contained in
these tables is shown below, corresponding to the space group Cmm2,
where C
means that the structure is described in terms of a lattice
centered on the faces separated by the c
axis. The first m
represents a mirror plane perpendicular to the
a
axis. The second m
means another mirror plane (in this case perpendicular to the second
main crystallographic direction), the b
axis. The number 2
refers to the two-fold axis parallel to the third
crystallographic direction, the c
axis.
Crystallographers
never get bored! Try to enjoy the beauty, looking for the symmetry of
the objects around you, and particularly in the objects
shown below ...
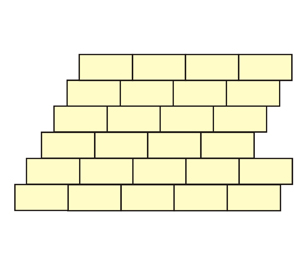
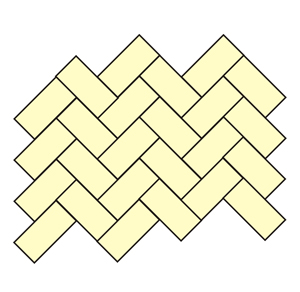
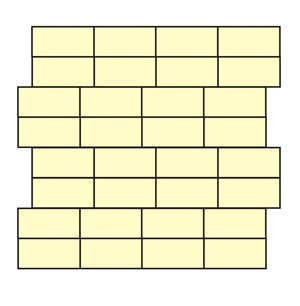
Look for possible unit-cells and symmetry
elements in these structures made with
bricks
(the solution is obtained clicking on
each
image)

Look for possible unit-cells and symmetry
elements in this drawing
(the solution is obtained after clicking
on the image)
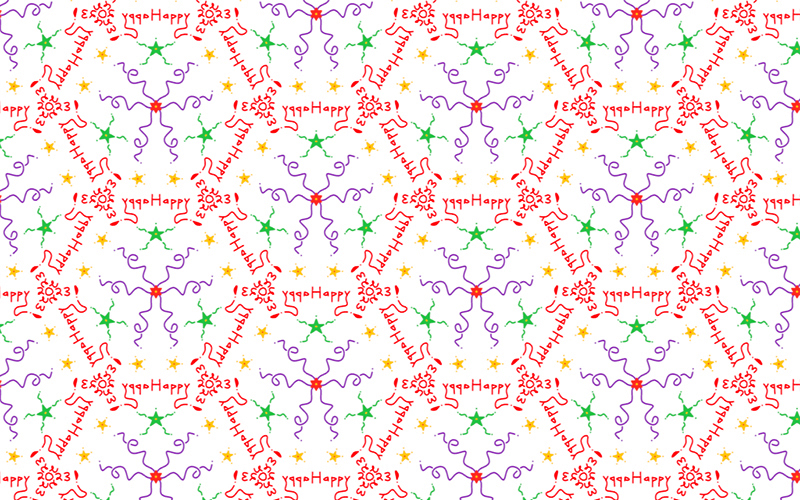
Look for possible unit-cells and symmetry
elements in this drawing
(the solution is obtained after clicking
on the image)

Look for possible unit-cells and symmetry
elements in this drawing
(the solution is obtained after clicking
on the image)
There
is a question
that surely the readers will have considered... In this chapter we have
shown elements of symmetry that operate inside the crystals, but we
have not yet said how we can find out the existence of such operations,
when in fact, and in the best of cases, we could only visualize the
external habit of the crystals if they are well formed! Although we
will not answer this question here, we can anticipate that this
response will be given by the behavior of the crystals when we
illuminate them with that special light that we know as X-rays,
but this will be the subject of another chapter.
In
any case, it doesn't end here! There are many more things to talk
about. Go on.
Next
chapter: Direct and reciprocal lattices
Table
of contents