The
amount of combinations of symmetry elements (point groups) passing
through the center of a finite body can be very high. However in
crystals, which inherently contain repetitions by translation, the
amount of combinations of symmetry elements is restricted to 32, called
"crystal classes"… (see also this link).
Figures below show the representations of the 32 crystal classes as shown in the International Tables for X-ray Crystallography:
Figures below show the representations of the 32 crystal classes as shown in the International Tables for X-ray Crystallography:
Crystal classes
(The centrosymmetric classes are marked with the word Laue)
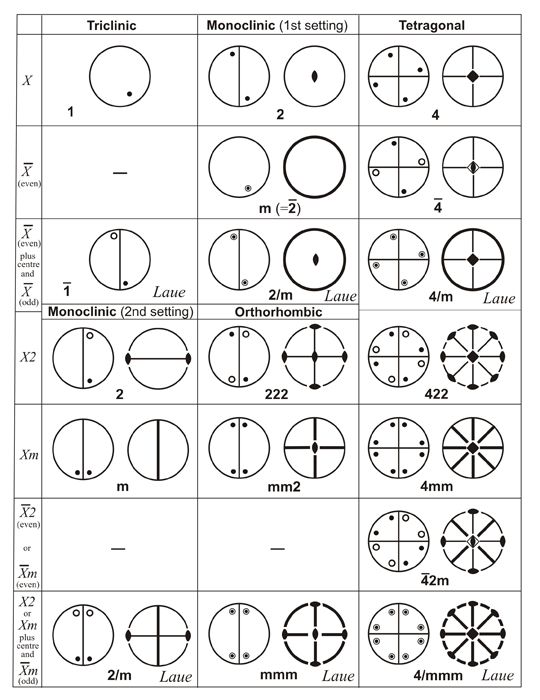
Stereograms of poles of the 32 Crystal Classes (first part) as they appear in
International Tables for X-ray Crystallography
(note that crystal class 2/m appears in two different orientations)
(z-axis is always normal to the drawing plane)
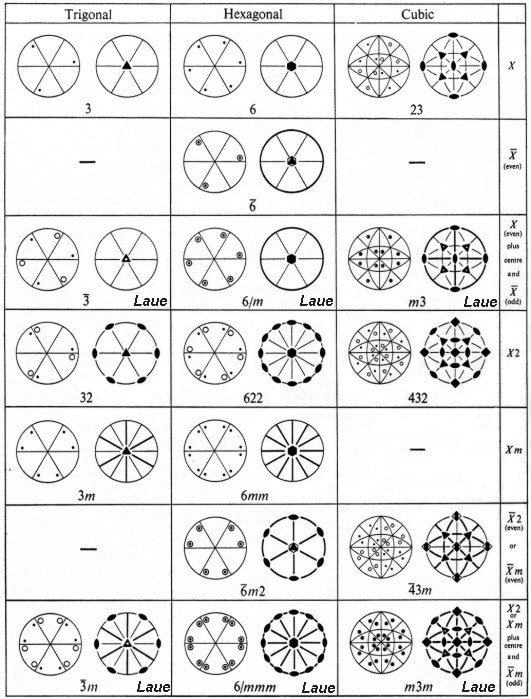
Stereograms of poles of the 32 Crystal Classes (second part) as they appear in
International Tables for X-ray Crystallography
(z-axis is always normal to the drawing plane)
