A model which has been "validated," according to the criteria described in another chapter, and which therefore shows:
- a reasonable agreement between observed and calculated structure factors,
- bond distances, bond angles and torsional angles that meet stereochemical criteria, and
- physically reasonable thermal vibration factors
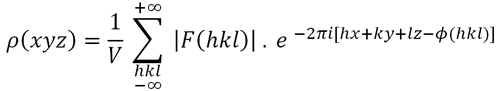
in which the atoms have been located and which is being affected by several conditions (see below)...
Regardless of the subjects included below, the experienced reader should also consult the contents of the comments included in the following articles:
The advanced reader, with interest in macromolecular crystallography, should also have a look to the results published in Nature (2016) 530, 202-206. This article shows that, in addition to the coherent diffraction (Bragg peaks), the diffraction patterns can display additional information in the form of continuous diffraction, very useful, among others, to increase the degree of resolution of the model. A brief summary of the article can be found through this link.
The effect of resolution
For instance, we must take into account the effect of the resolution level of the electron density function. The value that ρ(xyz) displays in each point in the unit cell is dependent on the sum of all structure factors (the waves diffracted by the atoms contained in the unit cell). Therefore, the amount of structure factors used in the sum, and their degree of observability, is an important aspect in obtaining a realistic value of the electron density at each point. The degree of precision (resolution level) of an electron density map is defined as the inverse of the distance that we would be able to "see" in the map, which is dependent on the radiation wavelength (λ) and on the maximum detection angle (θ). The minimum value of the "visible" distance (known as the resolution level, although actually is the inverse of the resolution level) can deduced from Bragg's Law:
λ / 2.sen θmax
Minimum "visible"
distance in an electron density map (also known
as resolution)
It seems obvious, therefore, that to
obtain a high resolution map (to see fine details of the
structure), we will need to use a small wavelength (small numerator)
and
to get diffraction data (structure factors) up to high diffraction
angles (large denominator).For crystals of low structural complexity, the number of structure factors available through a diffraction experiment is usually sufficient to obtain realistic values of ρ(xyz), and thus the map permits us to see structural details at high resolution (0.5 Angstroms or less), but this is not the usual case for macromolecules. For this reason, in all cases (but especially in protein crystals) the amount of experimental data is a crucial aspect.


Left: Low resolution: 5.0 Angström
Right: Medium resolution: 3.0 Angström

High resolution: 1.7 Angström

Constructing
a peptide segment on the electron density function obtained using
amplitudes and phases from a diffraction pattern with a resolution of
1.7 Angstrom.

Effect of resolution (amount of experimental data)
The
movie shows how the electron density map, in a
region of a
protein, changes as the resolution limit is adjusted from 0.5
to 6.0
Å, that is as the contribution of reflexions with the highest
Bragg angles is being omitted. For
this calculation the
phases are perfect and so are the amplitudes (R =
0,0%). Note that, even for a
perfect map (in terms of phases and amplitudes) one expects side chains
to poke out of density at 3.5 Å resolution.
Movie taken from EMBO
Bioinformatics Course.
The effect of amplitudes (intensities)
Similarly, to assess the reliability of a model one has take into account the effect of the precision attained for the diffraction amplitudes (intensity measurements):

The importance of amplitudes (precision attained by measuring intensities)
The
movie above displays the effect of calculating an electron
density map with "wrong" amplitudes. The images in the movie represent
the slow changing of all the amplitudes to a different set of randomly
selected values while phases are kept constant. The gradual change goes
from R=10% (reasonable disagreement) up to R=75% (random amplitudes). It
is interesting to note that the map hardly changes at all until the
R factor gets higher than 50%. The
resolution is 1.5 Å and the phases are always perfect.
Movie taken from EMBO
Bioinformatics Course.
The importance of phases
Finally, it should be noted that the parameter which most affects the reliability of a structural model is the correctness of the phases assigned to the diffraction amplitudes, as shown by the following movie.

The effect of phases (errors in the phases)
The
movie displays the effect of calculating a map with "wrong" phases.
The "figure of merit" (the cosine of the phases error) is displayed as
"m". The images are calculated by merging a perfectly calculated map
with
another map, calculated with the same amplitudes, but using phases
obtained from a model with randomly positioned atoms. By merging these
two maps amplitudes are always preserved but the phases change
slowly. The resolution is 1.5 Å and
the R-factor is always 0.0%. It
is important to note the strong dependence between the correctness
of
the phases and the accuracy of the map in order to recognize the atomic
positions.
Movie taken from EMBO
Bioinformatics Course.
But let's go back...
