 Tal y como ocurre con las ecuaciones
de Laue,
también la ley de Bragg puede deducirse de un
modo gráfico, muy intuitivo.
Tal y como ocurre con las ecuaciones
de Laue,
también la ley de Bragg puede deducirse de un
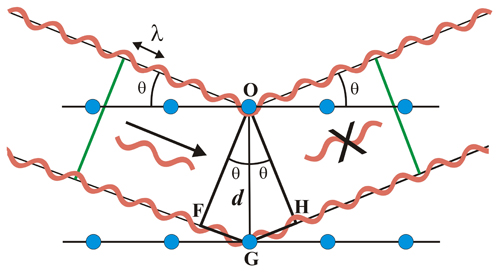
modo gráfico, muy intuitivo.La hipótesis de Bragg, propuesta por ambos, padre e hijo (William H. Bragg y William L. Bragg), consiste en imaginar la difracción como una reflexión de los rayos X originada por "espejos" imaginarios formados por planos de átomos de la red cristalina (mostrados como lineas horizontales que pasan por los centros dispersores, es decir, por los átomos que se muestran como círculos azules en la imagen de la izquierda). Debido a la naturaleza repetitiva del cristal, estos planos estarían separados entre sí por distancias constantes d.
En la figura de la izquierda, los dos haces de rayos X, de longitud de onda λ, inciden en fase sobre sendos "espejos" imaginarios (línea negras horizontales y paralelas), con un ángulo de incidencia θ, y formando un frente de ondas (línea verde de la izquierda).
Para que exista reflexión cooperativa es necesario que tras la reflexión ambos haces sigan estando en fase (linea verde de la derecha), situación que sólo ocurrirá si la diferencia de caminos recorridos por los frentes de onda OF y OH (frentes de onda, antes y después de la reflexión) corresponde a un número entero de veces la longitud de onda de la radiación incidente.
Esa condición equivale a decir, que la suma de los segmentos FG y GH corresponde a un número entero (n) de veces la longitud de onda (λ):
FG + GH
= n.
λ (1)
pero
FG = GH,
y sen
θ = FG
/ d
es decir:
FG
= d sen
θ
con lo que la expresión (1) se convierte en:
2 d sen θ = n. λ
que representa la bien conocida ley de Bragg.
Cuando los frentes de onda emergentes (tras la reflexión) están en oposición de fase, no se observará intensidad reflejada, es decir, que no se estará cumpliendo la ley de Bragg.
 Cuando el ángulo de
incidencia de los rayos X no
cumple la
ley de Bragg, los haces emergentes dejan de estar en fase
(línea verde de la derecha), y se anulan
entre sí, por lo que no se observará intensidad
reflejada.
Cuando el ángulo de
incidencia de los rayos X no
cumple la
ley de Bragg, los haces emergentes dejan de estar en fase
(línea verde de la derecha), y se anulan
entre sí, por lo que no se observará intensidad
reflejada.Si tenemos en cuenta la hipótesis de partida y nos fijamos con atención en esta última ecuación, resultará fácil darnos cuenta de que:
- Los planos reticulares se comportan como espejos que reflejan la "luz X" sólo en algunas posiciones dadas por:
θ = arc sen (n . λ / 2 . d)
- Para unas condiciones experimentales dadas (λ y d) se obtienen valores discretos del ángulo de difracción θ que corresponden a los diferentes valores del número entero n.
- No hay infinitos órdenes de difracción (sen θ ≤ 1) y su número máximo depende de las condiciones experimentales (cristal y longitud de onda):
nmax
= 2 . d
/ λ
- La "geometría" de la difracción (los ángulos de difracción θ) depende sólo de la geometría de la red, y no de la naturaleza de los átomos.

