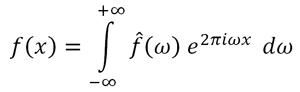Dispersión y
difracción.
Transformadas de Fourier

 La
transformada
de
Fourier,
denominada así por Jean-Baptiste
Joseph Fourier
(matemático
francés que vivió entre 1768 y 1830), es una herramienta matemática
casi mágica,
capaz de descomponer cualquier función periódica
(en tiempo, o en espacio) en una suma de funciones de
base de tipo sinusoidal (dependientes
de la frecuencia),
de manera similar
a cómo un acorde musical puede expresarse en
términos de las amplitudes (=volumen) de cada una sus notas
constitutivas.
La
transformada
de
Fourier,
denominada así por Jean-Baptiste
Joseph Fourier
(matemático
francés que vivió entre 1768 y 1830), es una herramienta matemática
casi mágica,
capaz de descomponer cualquier función periódica
(en tiempo, o en espacio) en una suma de funciones de
base de tipo sinusoidal (dependientes
de la frecuencia),
de manera similar
a cómo un acorde musical puede expresarse en
términos de las amplitudes (=volumen) de cada una sus notas
constitutivas.
El término transformada
de Fourier se refiere no sólo a la
propia operación de
transformación, sino también a la
función que produce.

Acorde
de DO MAYOR
C major chord, en notación
anglosajona
(do+mi+sol) = (C+E+G)
Un buen ejemplo es
lo que hace el oído
humano, ya que recibe una onda auditiva y la transforma,
descomponiéndola en distintas frecuencias (que es lo que
finalmente se escucha). El oído humano va percibiendo
distintas frecuencias a medida que pasa el tiempo, sin embargo, la
transformada de Fourier contiene todas las frecuencias del tiempo
durante el cual existió la señal; es decir, en la
transformada de Fourier
se obtiene un sólo espectro de frecuencias para toda la
función.
En definitiva, la transformada
de Fourier de una función periódica
en
el tiempo, es básicamente el espectro de frecuencias de
dicha función.
 Transformada
de Fourier entre dos
funciones.
La función f(x),
(1), es
dependiente del tiempo
(línea roja).
Es la suma de seis funciones sinusoidales con
diferente amplitud pero con
frecuencias armónicamente
relacionadas entre sí. La suma de dichas funciones se
denomina serie
de Fourier.
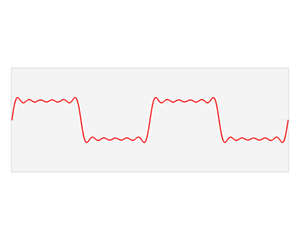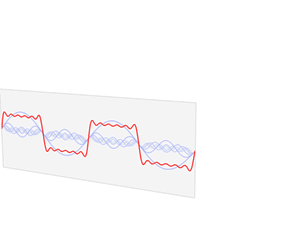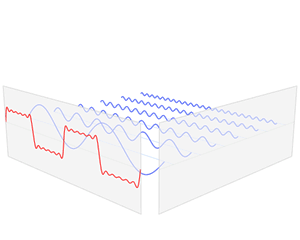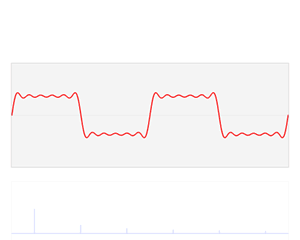
La transformada de Fourier
ˆf(ω), (2), (línea
azul) representa la amplitud vs. frecuencia, y
da
cuenta de las seis frecuencias y de sus correspondientes amplitudes.
Transformada
de Fourier entre dos
funciones.
La función f(x),
(1), es
dependiente del tiempo
(línea roja).
Es la suma de seis funciones sinusoidales con
diferente amplitud pero con
frecuencias armónicamente
relacionadas entre sí. La suma de dichas funciones se
denomina serie
de Fourier.
La transformada de Fourier
ˆf(ω), (2), (línea
azul) representa la amplitud vs. frecuencia, y
da
cuenta de las seis frecuencias y de sus correspondientes amplitudes.
(1) 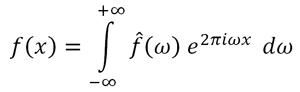
(2)

La función (2) es la
transformada de Fourier de la función (1)
La función (1) es la
transformada de Fourier inversa de la función (2)
Cada una de estas funciones de base en las que se puede descomponer una
función, es una exponencial
compleja con una frecuencia (ω)
diferente. Por lo tanto, la transformada
de Fourier nos proporciona una manera única de
expresar cualquier función complicada como la suma de
sinusoides
sencillas.
La
función inversa a una transformada
de Fourier se denomina transformada
de Fourier inversa,
también conocida como síntesis
de Fourier (también denominada serie
de Fourier), que es la forma mediante la cual
podemos obtener cualquier
función periódica original a partir de
la suma de sinusoides sencillas.
 El primero que aplicó las
propiedades de la transformada
de Fourier a los experimentos de difracción de
rayos X en los cristales
fue W.H.
Bragg en un artículo de 1915 (Phil. Trans., A,
215, 253-274).
El primero que aplicó las
propiedades de la transformada
de Fourier a los experimentos de difracción de
rayos X en los cristales
fue W.H.
Bragg en un artículo de 1915 (Phil. Trans., A,
215, 253-274).
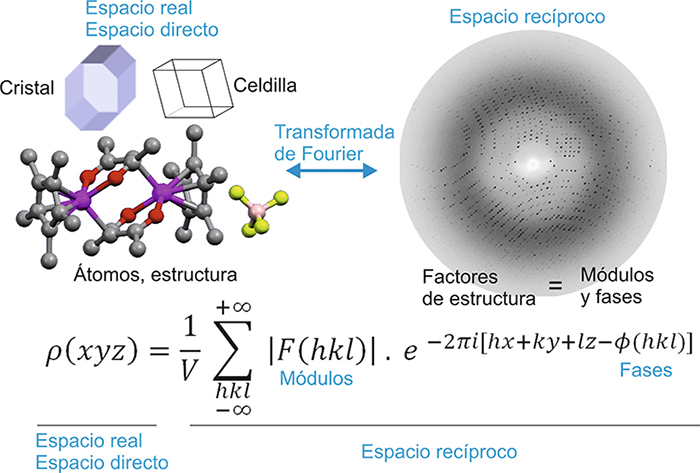
En otro capítulo de estas páginas veremos
cómo se usa la transformada
de Fourier para
pasar desde el denominado espacio directo, es
decir, el espacio en donde están los
átomos y las
moléculas (la función de densidad
electrónica
en los cristales), al espacio recíproco (el
patrón de difracción), y viceversa. Entre ambos
espacios, es decir,
entre las dos funciones matemáticas que los definen, hay una
transformada de Fourier,
aspecto que ya se discutirá en otros capítulos...
Es necesario recordar que la transformada de Fourier ha
sido una de las herramientas fundamentales patra el desarrollo de la
cristalografía moderna, y merece la pena leer el excelente
artículo sobre el legado de J.-B. J Fourier.
 La
transformada
de
Fourier,
denominada así por Jean-Baptiste
Joseph Fourier
(matemático
francés que vivió entre 1768 y 1830), es una herramienta matemática
casi mágica,
capaz de descomponer cualquier función periódica
(en tiempo, o en espacio) en una suma de funciones de
base de tipo sinusoidal (dependientes
de la frecuencia),
de manera similar
a cómo un acorde musical puede expresarse en
términos de las amplitudes (=volumen) de cada una sus notas
constitutivas.
La
transformada
de
Fourier,
denominada así por Jean-Baptiste
Joseph Fourier
(matemático
francés que vivió entre 1768 y 1830), es una herramienta matemática
casi mágica,
capaz de descomponer cualquier función periódica
(en tiempo, o en espacio) en una suma de funciones de
base de tipo sinusoidal (dependientes
de la frecuencia),
de manera similar
a cómo un acorde musical puede expresarse en
términos de las amplitudes (=volumen) de cada una sus notas
constitutivas. 

 Transformada
de Fourier
Transformada
de Fourier