If, after reflection, emerging waves are
in
phase, reflected intensity will be observed, ie, Bragg's Law
is fulfilled.
 As it was shown
with Laue
equations, Bragg's Law proposed by both, father and
son (William
H. Bragg and William
L. Bragg), may
also be derived graphically in an easy way...
As it was shown
with Laue
equations, Bragg's Law proposed by both, father and
son (William
H. Bragg and William
L. Bragg), may
also be derived graphically in an easy way...
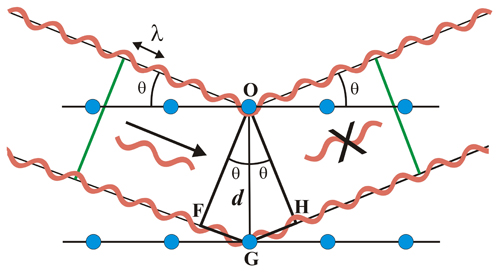
The hypothesis is to imagine Bragg's diffraction as a reflection of X-rays on the surface of imaginary "mirrors" formed by atomic planes in the crystal lattice (shown as horizontal lines containing scattering centers, that is, atoms shown as blue circles in the left image). Due to the repetitive nature of the crystal, these planes would be separated by a constant distance d.
The two X-ray beams of wavelength λ, arrive in phase onto the respective imaginary planes, with an angle of incidence θ, and form a wave front (green line on the left).
In order to obtain a cooperative effect, after reflection both X-ray beams should still be in phase (green line on the right), a situation that will only happen if the difference of path traveled by the wave fronts OF and OH (wavefronts before and after reflection) corresponds with an integer number of wavelenghts.
This condition is equivalent to say that the sum of the FG and GH segments corresponds to an integer (n) times the wavelength (λ):
If the emerging reflected waves have opposite phase, no reflected intensity will be observed, ie, Bragg's Law is not fulfilled.
 When
the angle of incidence of
the X-rays does not satisfy the Bragg's Law, the emergent beams are no
longer in phase (green line on the right), and cancel each other, so
that no reflected intensity will be observed.
When
the angle of incidence of
the X-rays does not satisfy the Bragg's Law, the emergent beams are no
longer in phase (green line on the right), and cancel each other, so
that no reflected intensity will be observed.
If we consider the baseline scenario and look carefully at the Bragg's equation, it is easy to realize that:
 As it was shown
with Laue
equations, Bragg's Law proposed by both, father and
son (William
H. Bragg and William
L. Bragg), may
also be derived graphically in an easy way...
As it was shown
with Laue
equations, Bragg's Law proposed by both, father and
son (William
H. Bragg and William
L. Bragg), may
also be derived graphically in an easy way...The hypothesis is to imagine Bragg's diffraction as a reflection of X-rays on the surface of imaginary "mirrors" formed by atomic planes in the crystal lattice (shown as horizontal lines containing scattering centers, that is, atoms shown as blue circles in the left image). Due to the repetitive nature of the crystal, these planes would be separated by a constant distance d.
The two X-ray beams of wavelength λ, arrive in phase onto the respective imaginary planes, with an angle of incidence θ, and form a wave front (green line on the left).
In order to obtain a cooperative effect, after reflection both X-ray beams should still be in phase (green line on the right), a situation that will only happen if the difference of path traveled by the wave fronts OF and OH (wavefronts before and after reflection) corresponds with an integer number of wavelenghts.
This condition is equivalent to say that the sum of the FG and GH segments corresponds to an integer (n) times the wavelength (λ):
FG + GH
= n.
λ (1)
but FG = GH
and sin
θ = FG
/ d
that is:
FG
= d sen
θ
and therefore expression (1)
becomes:2 d
sin θ = n.
λ
This is the Bragg's Law.
If the emerging reflected waves have opposite phase, no reflected intensity will be observed, ie, Bragg's Law is not fulfilled.
 When
the angle of incidence of
the X-rays does not satisfy the Bragg's Law, the emergent beams are no
longer in phase (green line on the right), and cancel each other, so
that no reflected intensity will be observed.
When
the angle of incidence of
the X-rays does not satisfy the Bragg's Law, the emergent beams are no
longer in phase (green line on the right), and cancel each other, so
that no reflected intensity will be observed.If we consider the baseline scenario and look carefully at the Bragg's equation, it is easy to realize that:
- The lattice planes behave like mirrors reflecting the 'X-light" only in certain positions given by:
θ = sin-1
(n . λ / 2 . d)
- For given experimental conditions (λ and d) only discrete values of the diffraction angle θ are obtained, that correspond to the different values of the integer n.
- There are only a finite number of diffraction orders (as sin θ ≤ 1) and the maximum number of them depends on the given experimental conditions (crystal and wavelength):
- The geometry of diffraction (ie the diffraction angle θ) depends on the lattice geometry only.

